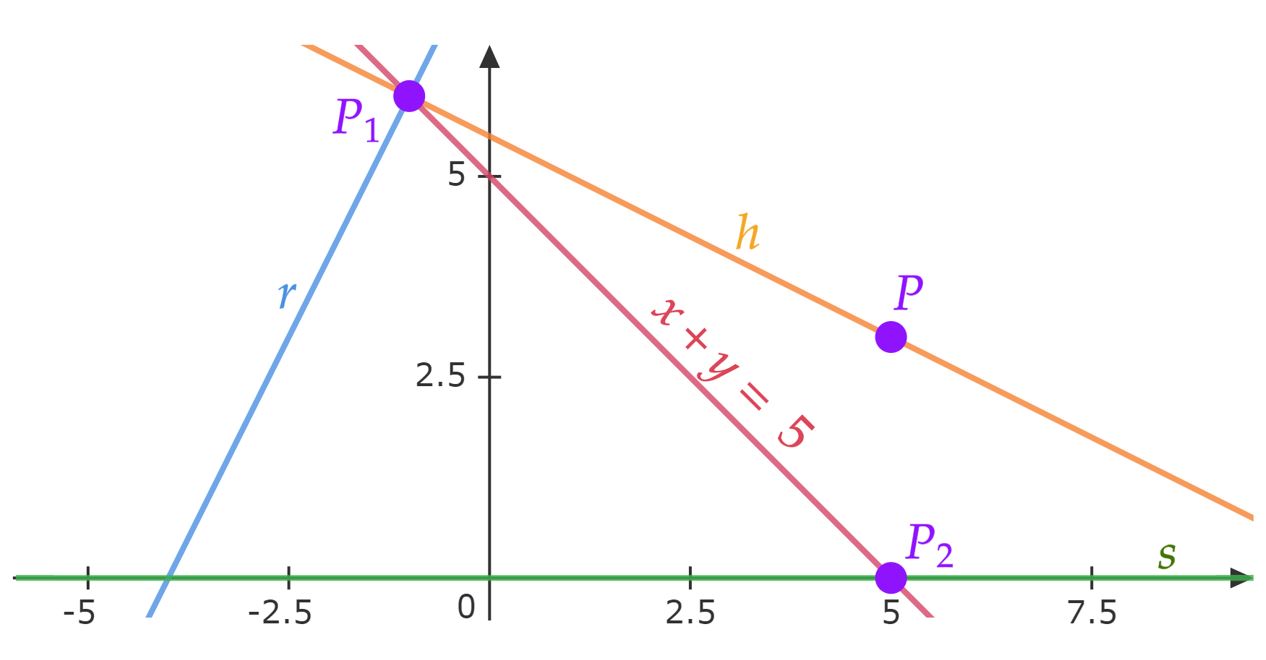
Dados os pontos , e , sejam e as retas tais que , , . Considere e os pés das retas perpendiculares traçadas de às retas e , respectivamente. Então a equação da reta que passa por e é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Não é difícil perceber que a equação da reta $s$ é o eixo das abscissas, isto é, $s: y =0$. Já a reta $r$, podemos aplicar a condição de alinhamento entre três pontos: \begin{matrix} \begin{vmatrix}
x & y \\
0 & 8 \\
-4 & 0 \\
x & y
\end{vmatrix} = 0 &\Rightarrow& r: 2x - y + 8 = 0 &,& m_r = 2
\end{matrix}O pé da perpendicular de $s$ é bem simples, será $P_2 : (5,0)$ vide o ponto $P$. Por outro lado, o pé da perpendicular de $r$ será mais trabalhoso, primeiro encontremos essa reta perpendicular, denotemos ele de $h$, visto o coeficiente angular de $r$ $(m_r)$, sabemos que o coeficiente angular de $h$ será $m_h = -1/2$ . Nessa perspectiva, como a perpendicular passa pelo ponto $P$, temos:
\begin{matrix} m_h = \dfrac{(y-5)}{(x-3)} &\Rightarrow& h: x+2y - 11 = 0
\end{matrix} $P_1$ será o ponto de intersecção entre a reta $r$ e $h$, \begin{matrix} P_1 : (-1 , 6)
\end{matrix}Por fim, num raciocínio análogo ao do início, temos a reta que passa por $P_1$ e $P_2$ como: \begin{matrix} \begin{vmatrix}
x & y \\
-1 & 6 \\
5 & 0 \\
x & y
\end{vmatrix} = 0 &\Rightarrow& \fbox{$ x+y =5$}\end{matrix}
 \begin{matrix} Letra \ (A)
\end{matrix}
\begin{matrix} Letra \ (A)
\end{matrix}

Ampliar Imagem

