Planificando a situação descrita, têm-se: 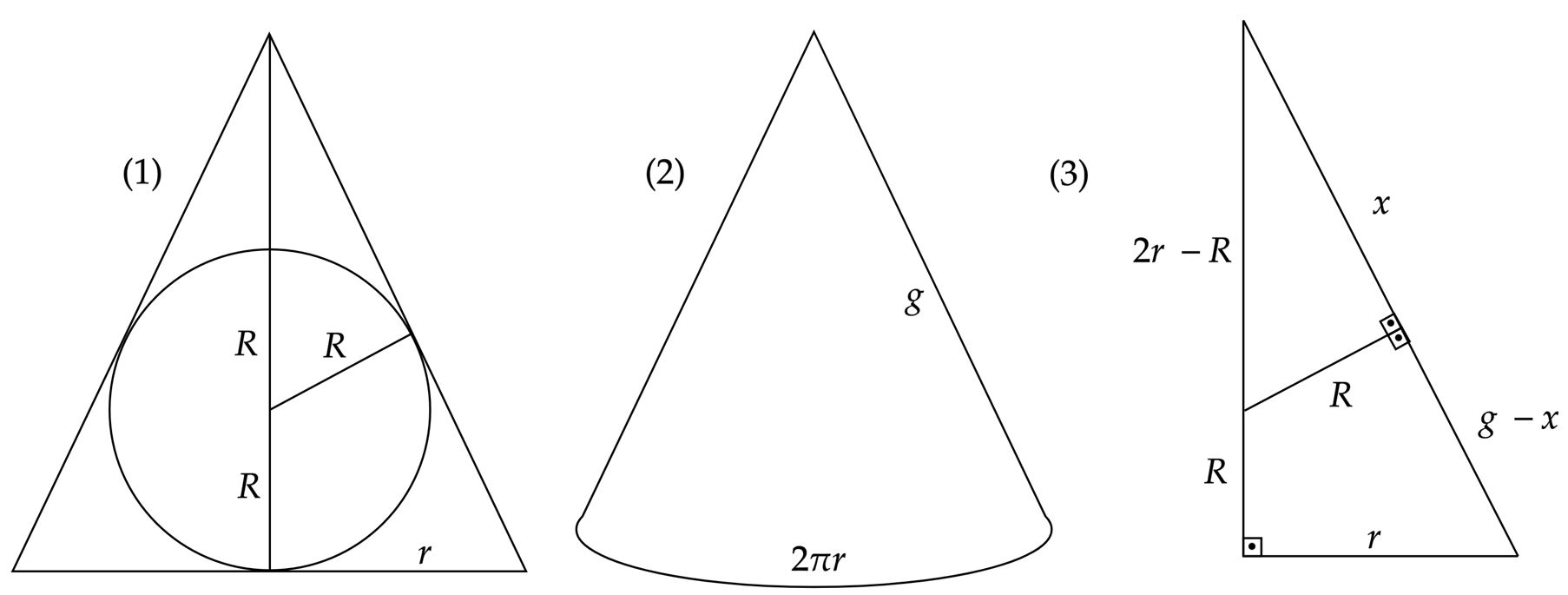Analisando o item $(3)$ por Pitágoras no triângulo maior, têm-se: \begin{matrix} g^2 = r^2 + (2r)^2 &\therefore& \fbox{$g = r \sqrt{5}$} \end{matrix}Veja que, no item $(2)$, a área do setor circular é a área lateral do cone, então: \begin{matrix} A_{área \ lateral} = \pi \cdot r \cdot g &\Rightarrow& A_{área \ lateral} = \pi \cdot r^2 \sqrt{5} &(4) \end{matrix}Novamente, analisando o item $(3)$, façamos uma semelhança de triângulos: \begin{matrix} {{\dfrac{2r - R}{R } }} ={{\dfrac{g}{2r} }} &\therefore& \fbox{$ r = R \cdot {{ \left(\dfrac{\sqrt{5} + 1}{2} \right)}} $} \end{matrix}Por fim, substituindo nosso resultado acima em $(4)$: \begin{matrix} A_{área \ lateral} = \pi \cdot R^2 \cdot (\sqrt{5} + 1)^2 \cdot {{\dfrac{\sqrt{5}}{4} }} \ \pu{cm^2} & \tiny{\blacksquare} \end{matrix} \begin{matrix} Letra \ (B) \end{matrix}