A priori, vamos "enxergar" a situação descrita, na figura abaixo: $(1)$ representa a seção meridiana, enquanto $(2)$ o setor circular (planificação da área lateral do cone), e por fim, $(3)$ o cone. 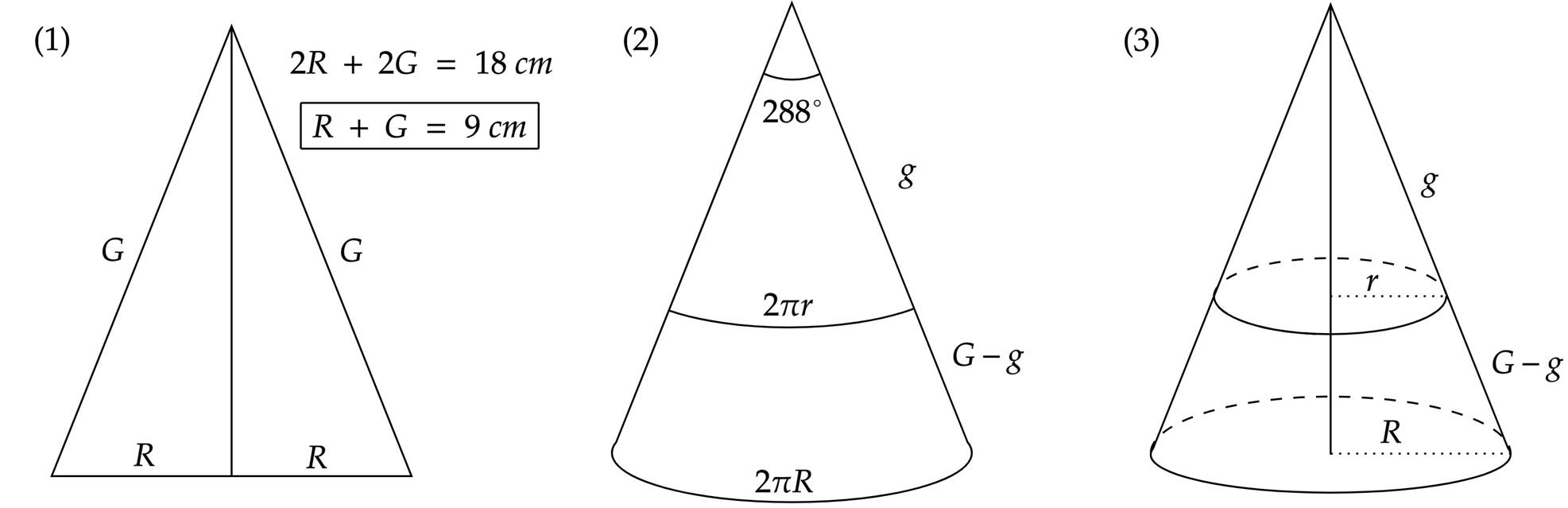Repare no item $(2)$ da imagem acima, sabe-se que a área deste setor circular é igual a área lateral do cone, com isso: \begin{matrix} A_{setor} = A_{lateral \ cone} &\Rightarrow& \pi \cdot R \cdot G = {{ \left(\dfrac{288^{\circ}}{360^{\circ}} \right)}} \cdot \pi \cdot G^2 &\therefore& 45R = 36G \end{matrix}Perceba que, substituindo o resultado que encontramos no item $(1)$ da figura, têm-se: \begin{matrix}45R = 36(9-R) &\therefore& \fbox{$R = 4 \ \pu{cm}$} &\Rightarrow& \fbox{$G = 5\ \pu{cm}$} \end{matrix}Pelo último período do enunciado, sabemos a razão entre as bases do tronco, logo: \begin{matrix} {{\dfrac{B_{menor}}{B_{maior}} }} = {{\dfrac{\pi r^2}{\pi R^2} }} = {{\dfrac{4}{9} }} = k^2 &\therefore& \fbox{$r = {{\dfrac{8}{3}}} \ \pu{cm}$} &,& \fbox{$k = {{\dfrac{2}{3}}} $} \end{matrix}Por $k$ temos a razão entre linhas, isto é: \begin{matrix} {{\dfrac{g}{G} }} = k &\therefore& \fbox{$g = {{\dfrac{10}{3}}} \ \pu{cm}$} \end{matrix}Volte a observar a figura $(2)$, dela pode-se encontrar a área lateral do tronco, por uma analogia com a área de um trapézio, veja: \begin{matrix} A_{lateral \ tronco} = { {\dfrac{ (2\pi R + 2\pi r) \cdot (G -g) }{ 2 } }} = \pi \cdot {{ \left(\dfrac{100}{9} \right)}} \ \ \pu{cm^2} \end{matrix}Ora, a área total do tronco de cone é a área lateral mais a área de suas respectivas bases, portanto: \begin{matrix} A_{total} = A_{lateral \ tronco} + B_{maior} + B_{menor} \\ \\ A_{total} = \pi \cdot {{ \left(\dfrac{100}{9} \right)}} + \pi {{ \left(\dfrac{8}{3} \right)}}^2 + \pi4^2 \\ \\ A_{total} = \pi \cdot {{ \left(\dfrac{308}{9} \right)}} \ \pu{cm^2} \\ \\ Letra \ (B) \end{matrix}