A questão requer o conhecimento das propriedades do logaritmo, assim como o entendimento do círculo trigonométrico. Veja as propriedades do logaritmo que serão usadas: \begin{matrix} \log{a} - \log{b} = \log{a/b} &,& \dfrac{\log{a}}{\log{b}} = \log_b{a} &,& a^{{\large{\log_a b}}} = b \end{matrix}Com isso, podemos manipular $\alpha$ para um termo mais conveniente, veja:\begin{matrix} \alpha &=& \dfrac{1}{2} \left( \dfrac{\log{2}}{\log{2/3}} \right) &=& \dfrac{1}{2}(\log_{2/3}{2}) \end{matrix}Analisando desigualdade, têm-se:\begin{matrix} 2^{\sin{x}} \le \left( \dfrac{2}{3} \right)^{ {\large{\frac{1}{2}(\log_{2/3}{2})}}} &\Rightarrow& 2^{\sin{x}} \le 2^{{\large{\frac{1}{2}}}} &\therefore& \sin{x} \le \dfrac{1}{2} \end{matrix}Agora, tudo se baseia numa análise do circulo trigonométrico, veja: 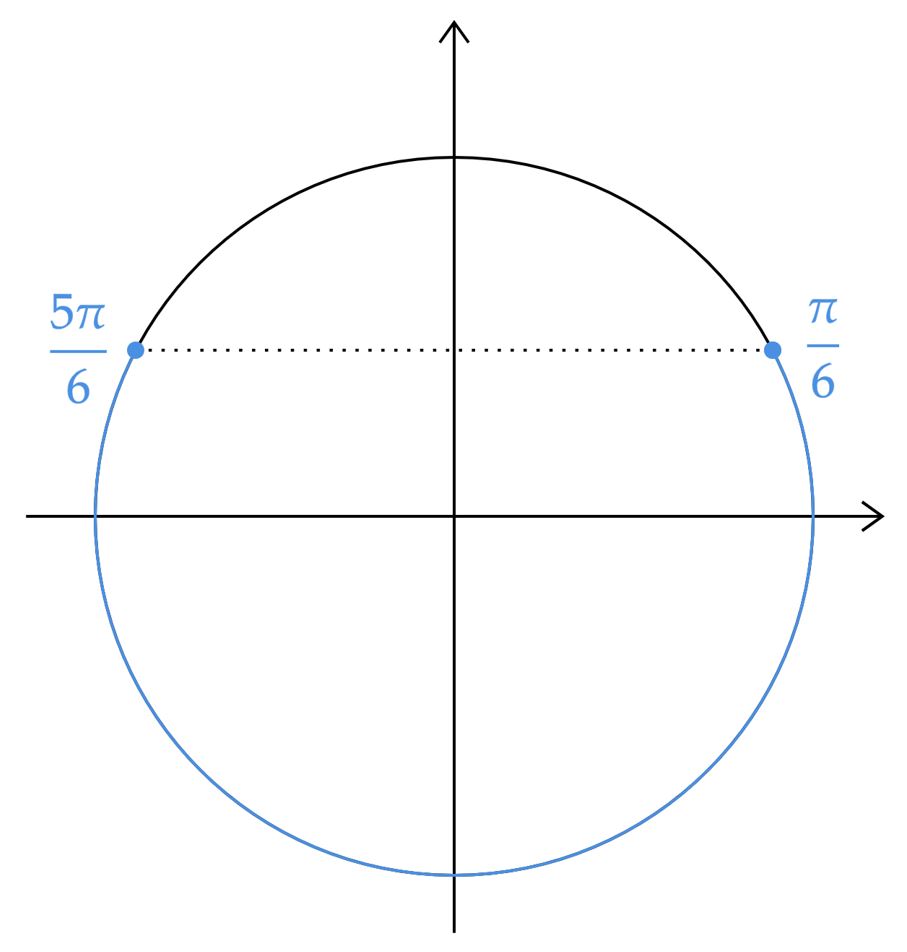Com isso, não é difícil definir o conjunto solução como: \begin{matrix} \left[ 0 , \dfrac{\pi}{6} \right] &\cup& \left[ \dfrac{5\pi}{6} , 2\pi \right) \end{matrix}\begin{matrix} Letra \ (D) \end{matrix}

$2^{\sin x} \leq \left( \dfrac{2}{3}\right)^\alpha$ $\therefore$ $\log 2^{\sin x} \leq \log \left( \dfrac{2}{3}\right)^\alpha$ $\sin x \cdot \log 2 \leq \alpha \cdot \log \left( \dfrac{2}{3}\right)$ $\sin x \cdot \log 2 \leq \dfrac{1}{2} \cdot \dfrac{\log 2}{(\log 2 - \log 3)} \cdot \log \left( \dfrac{2}{3}\right)$ $\sin x \cdot \log 2 \leq \dfrac{1}{2} \cdot \dfrac{\log 2}{\log \left( \dfrac{2}{3}\right)} \cdot \log \left( \dfrac{2}{3}\right) = \dfrac{\log 2}{2} \geq \sin x \log 2$ $\implies \sin x \leq \dfrac{1}{2} $ Portanto o conjunto solução da desigualdade $2^{\sin x} \leq \left( \dfrac{2}{3}\right)^\alpha$ no intervalo $[0,2\pi]$ é $[0,\pi/6] \cup [5\pi /6 , 2\pi)$ $\text{Resposta : Alternativa D}$