Uma haste rígida de peso desprezível e comprimento , carrega uma massa em sua extremidade. Outra haste, idêntica suporta uma massa em seu ponto médio e outra massa em sua extremidade. As hastes podem girar ao redor do ponto fixo , conforme a figura.
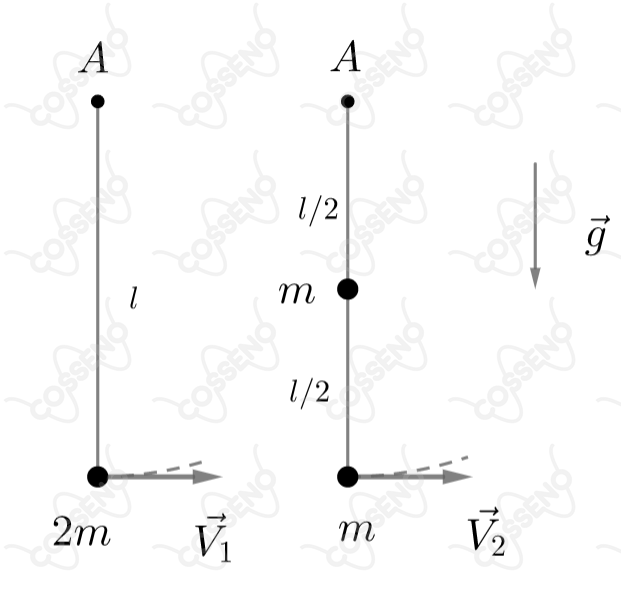
Qual a velocidade horizontal mínima que deve ser comunicada às suas extremidades para que cada haste deflita até atingir a horizontal ?
Na primeira barra:
Aplicando a Conservação de Energia: $$\begin{align}\Delta E &= 0\\ Em_0 &= Em_f\\ Ec_0 + Ep_0 &= Ec_f + Ep_f\end{align}$$
Sendo a altura inicial nula, por ser o nível do "solo" e a velocidade final zero, pois o objeto para na horizontal, ficamos:$$\frac{2mv_0^2}{2} = 2mg\ell \Rightarrow \boxed{v_0 = \sqrt{2g\ell}}$$
Na segunda barra:
Nesse caso há dois objetos se movendo e os dois irão transladar junto com a haste.
Aplicando a Conservação de Energia: $$\frac{mv_1^2 + mv_2^2}{2} = mg\ell + \frac{mg\ell}{2} \\ v_1^2 +v_2^2 = 3g\ell \quad \star (1)$$
Contudo, as duas massas giram com velocidade angular constante e iguais, então: $$\omega_1 = \omega_2 \\ \frac{v1}{r1} = \frac{v2}{r2} \\ v_1 = 2v_2$$
E aplicando em $\star (1)$: $$v_2 = \sqrt \frac{12g\ell}{15} = \boxed{\sqrt{2{,}4g\ell}}$$
Gabarito $\text{Gabarito D)}$
$\clubsuit$ Observação
Sobre a segunda barra: $v_1$ é o objeto com altura $\frac{\ell}{2}$ e $v_2$ é o com altura $\ell$, em relação ao ponto $\text{A}$.
