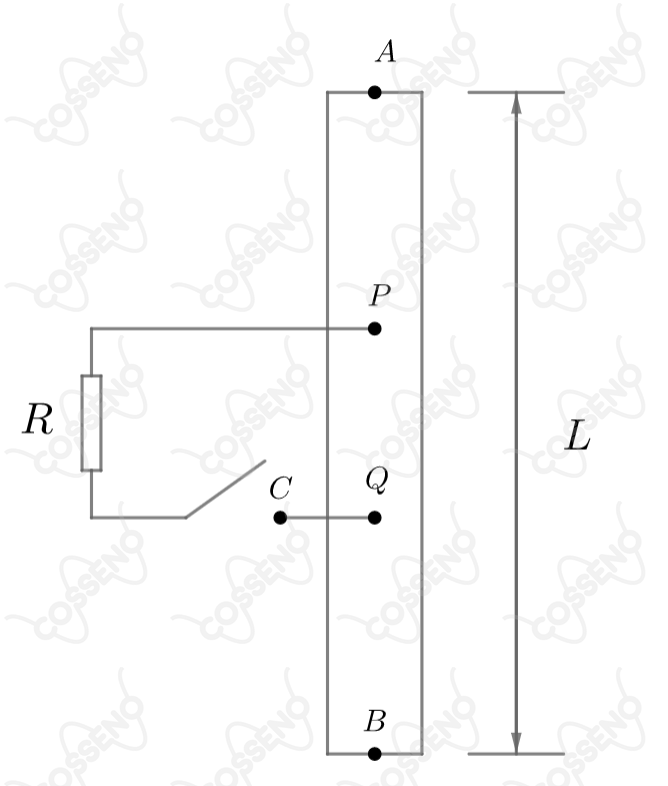
Na figura, representa um resistor filiforme, de resistência e comprimento . As distâncias e são e , respectivamente. A resistência vale . Quando a chave está aberta, a corrente constante passa por . Quando a chave for fechada, a corrente que entrará em será:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Quando a chave está aberta, temos a corrente passando pelo resistor filiforme $AB$, assim, segundo a $\text{Primeira Lei de Ohm}$: \begin{matrix} \Delta V_{AB} = 6r \ (1)
\end{matrix}
A partir do momento que fechamos a chave, constatamos um resistor paralelo ao segmento de fio $PQ$. Dessa forma, com conhecimento da $\text{Segunda Lei de Ohm}$, sabemos que a resistência de cada parte do fio é proporcional ao comprimento do mesmo, veja:\begin{matrix} r = \large{\frac{\rho . L}{A}} &\Rightarrow& r_{AP} = 0,4r &,& r_{PQ} = 0,4r &,& r_{QB} = 0,2r
\end{matrix}Dos segmentos paralelos, \begin{matrix} \large{\frac{1}{r_{eq}} = \frac{1}{r_{PQ}} + \frac{1}{R} } &\therefore& r_{eq} = 0,2r
\end{matrix}Assim, a resistência equivalente total, \begin{matrix}r_T = r_{eq} + r_{AP} +r_{QB} &\therefore& r_{T} = 0,8r
\end{matrix}Logo, $d.d.p$: \begin{matrix} \Delta V_{AB} = r_T.i \ (2)
\end{matrix}Analisando $(1)$ e $(2)$: \begin{matrix} \fbox{$i = 7,5 \ A$} \\ \\ Letra \ (A)
\end{matrix}

02:14 04/05/2024
Olá, porque VAB do circuito com a chave aberta é igual a VAB com a chave fechada?

14:22 16/05/2024
Vab é definido por uma fonte de tensão externa. Essa fonte n é alterada quando se muda a resistência total do sistema

