Uma corda de comprimento e massa está presa em ambas as extremidades sob tensão . Nestas condições, a freqüência fundamental de vibração desta corda é:
Com conhecimento da $\text{Equação de Taylor}$, temos:
\begin{matrix} v = \large{\sqrt{\frac{F}{\mu}}} &,& \mu = \large{\frac{m}{l}} &\Rightarrow& \fbox{$v = 200 \ m/s$}
\end{matrix}De uma corda vibrando em sua frequência fundamental, sabemos:
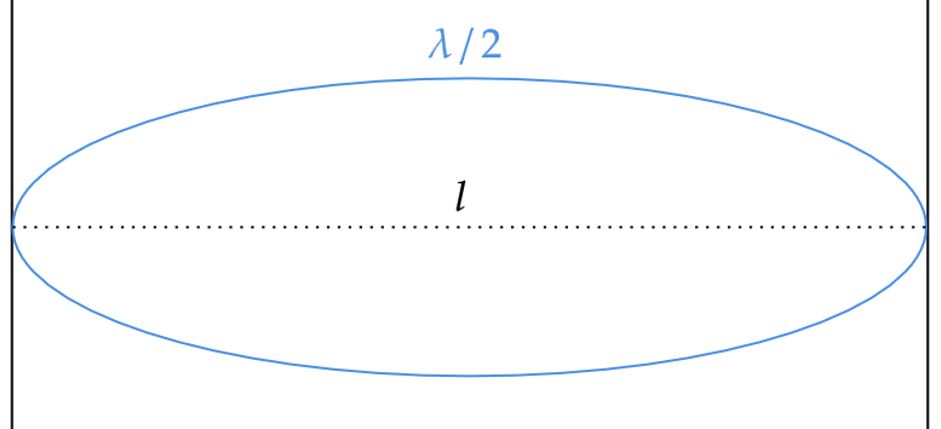Então,
\begin{matrix} l = \large{\frac{\lambda}{2}} &\Rightarrow& \fbox{$\lambda = 1 \ m$}
\end{matrix}Da equação fundamental da ondulatória:
\begin{matrix} v = \lambda . f &\Rightarrow& \fbox{$f = 200 \ Hz$}
\end{matrix}
\begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
