Pela geometria do problema, mais precisamente o triângulo $ABC$, não é difícil dizer que $\overline{AC} = \overline{BC}$, visto que o triângulo é isósceles. Nessa perspectiva, a tração $T_{AC}$ é igual a tração $T_{BC}$, em que o enunciado chama de $T$. Com isso, denotemos a tração entre o bloco e o fio de $F_T$, em que têm-se no equilíbrio: \begin{matrix} \vec{T_{AC}} + \vec{T_{BC}} = \vec{F_{T}} &,& |\vec{T_{AC}}| = |\vec{T_{BC}}| = T \end{matrix}Decompondo as forças em eixos vertical e horizontal, pode-se perceber que: 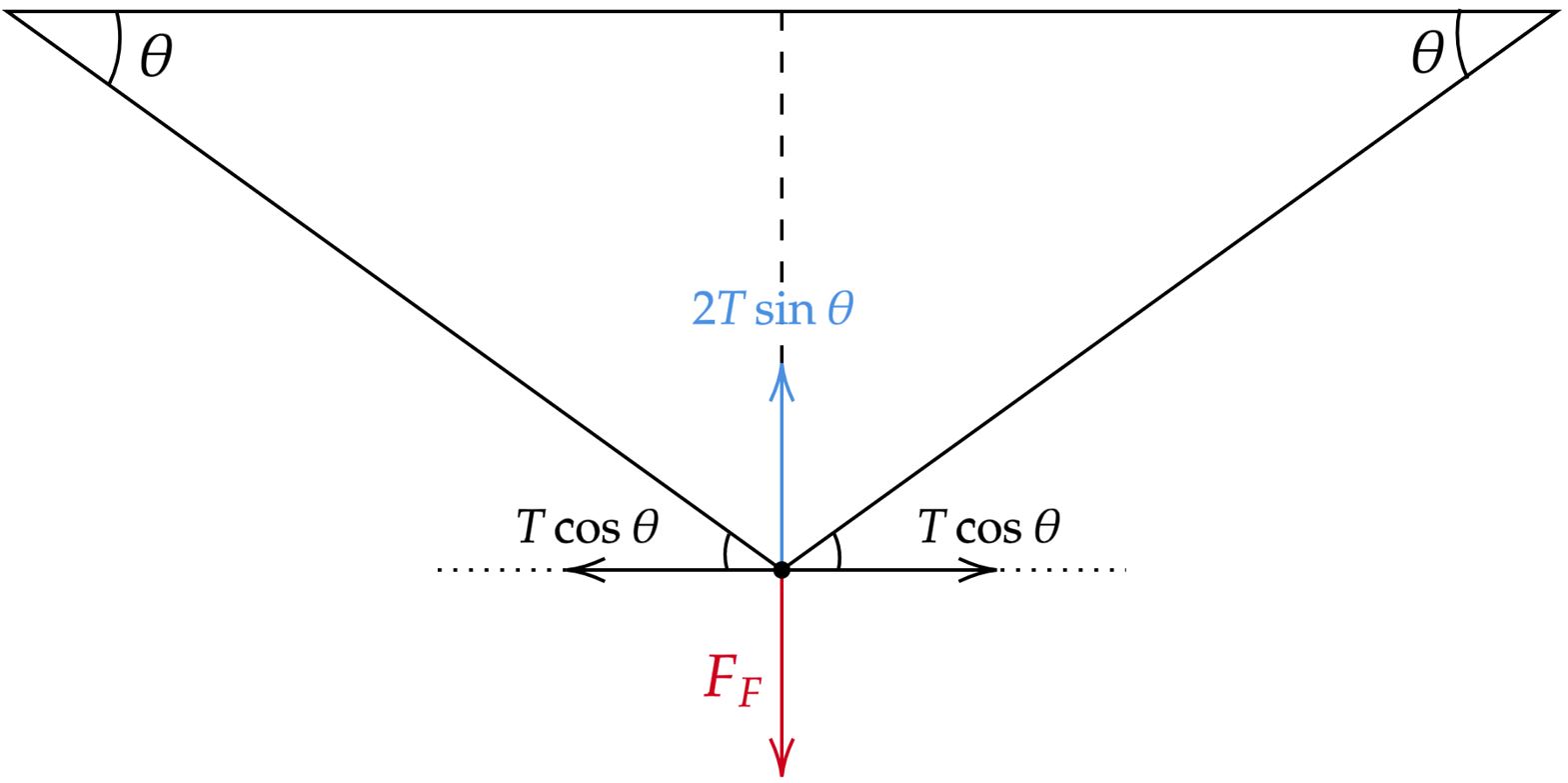\begin{matrix} 2T\sin{\theta} = F_T &,& \underbrace{F_T = P}_{\text{Equilíbrio do bloco}} &\therefore& T = \dfrac{P}{2\sin{\theta}} & \tiny{\blacksquare} \end{matrix}