A figura representa uma vista aérea de um trecho retilíneo de ferrovia. Duas locomotivas a vapor, e , deslocam-se em sentidos contrários com velocidades constantes de e , respectivamente. Uma vez que corresponde ao rastro da fumaça do trem , ao rastro da fumaça de e que , determine a velocidade(em ) do vento. Despreze as distâncias entre os trilhos de e .
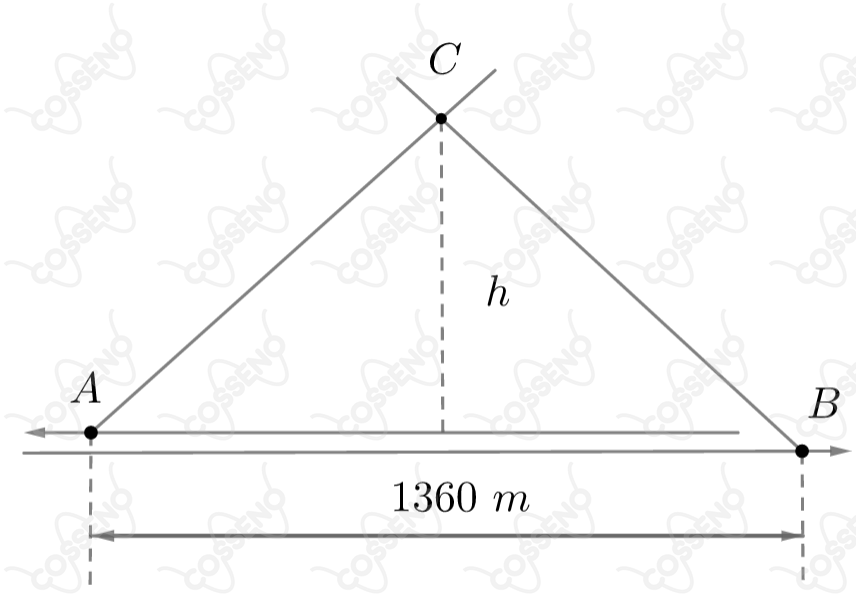
$h=160\ m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, devemos supor que após a fumaça ser expelida apenas o vento atue sobre ela. Dessa forma, vamos focar na primeira nuvem de fumaça atirada ao ar, ela deve chegar no ponto C no momento retratado na figura do enunciado. \begin{matrix} V_A: \ 50,4 \ km/h \ \rightarrow \ 14m/s &,& V_B: \ 72,0 \ km/h \ \rightarrow \ 20m/s
\end{matrix}Repare que, no momento inicial, os dois trens estavam em uma mesma posição que chamaremos de $X$, como $A$ é menos veloz que $B$, $X$ deve estar entre $A$ e o ponto médio de $\overline{AB}$, que denotaremos por $D$. Prosseguindo: \begin{matrix} \overline{AX} + \overline{XB} = \overline{AB} &\Rightarrow& V_A. t + V_B.t = 1360 &\therefore& t = 40s
\end{matrix}Perceba que, $40s$ é o tempo necessário para a nossa primeira nuvem de fumaça chegar até $C$. Por outro lado, $40s$ é o tempo que o vento leva para guiar a nossa nuvem até $C$ pela trajetória $\overline{XC}$.
$\color{orangered}{Obs:}$ Vale ressaltar que, $\overline{XC}$ também indica a direção do vendo.
Precisamos encontrar $\overline{XC}$, entretanto, antes careceremos de encontrar $\overline{XD}$, veja que: \begin{matrix} \overline{AD} - \overline{AX} = \overline{XD} &\Rightarrow& 680 - V_A. t = \overline{XD} &\therefore& \overline{XD} =120m
\end{matrix}Podemos agora aplicar um simples Pitágoras: \begin{matrix} h^2 + \overline{XD}^2 = \overline{XC}^2 &\therefore& \overline{XC} =200m
\end{matrix}Por fim, sabemos que a trajetória da nossa nuvem é guiada pelo vento, a nuvem por sua vez percorrerá $\overline{XC}$, e chegará em $C$ após $40s$, assim: \begin{matrix}V_{nuvem} = V_{vento} = {\large{\frac{\overline{XC}}{t}}} = {\large{\frac{200}{40}}} &\therefore& V_{vento} = 5m/s
\end{matrix}\begin{matrix} Letra \ (A)
\end{matrix}
Solução 3
Pelo enunciado tem se que: $$V_A = 50,4 km/h = 14m/s$$
$$V_B = 72,0 km/h = 20m/s$$
Portanto a velocidade relativa das locomotivas é $V_r = 20 - -14 = 34 m/s$
Logo o espaço de $1360m$ foi percorrido em $1360 \div 34 =40s$
Observa-se pelo enunciado, que no eixo $y$ a fumaça deslocou $160m$ nesse mesmo período de tempo, logo a velocidade $V_y$ do vento é $V_y = 160 \div 40 = 4 m/s$
Sabe-se pelo enunciado que o triângulo formado pelo rastro é isósceles, logo distâncias iguais são percorridas pelo vento $$V_{va} = \dfrac{1360\div 2}{14+x} = V_{vb} = \dfrac{1360\div 2}{20-x}$$
Portanto $V_x = 3 m/s$
Por pitágoras $$V_v = \sqrt{V_x^2 + V_y^2} = 5m/s$$
Alternativa (A).
Solução 2:
O primeiro passo é adotar um eixo de deslocamento no horizontal, para isso, considere o ponto $A$ como a origem e o ponto $B$ como $1360 \ m$. O bizu agora é o seguinte: pense que a locomotiva $B$ está inicialmente em $A$ e a locomotiva $A$ em $B$ e irão se encontrar em um ponto $E$ entre o ponto $B$ e o ponto médio de $\overline{AB}$.
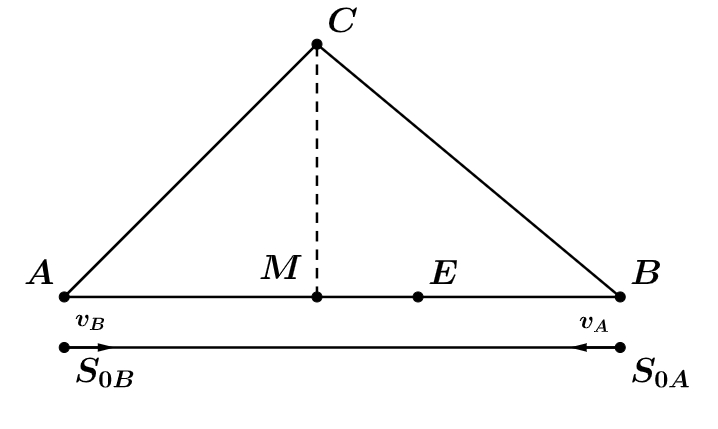 Escrevendo as equações da cinemática para cada uma das locomotivas, obtemos:
$$S_{A} = 1360 - 14t\\
S_{B} = 0 + 20t.$$
Como as locomotivas irão se encontrar, basta igualar a posição de ambos e encontrar o tempo em que tal evento ocorrerá.
$$1360 - 14t = 20t \Rightarrow t = 40 \ s$$
Para encontrar a posição de encontro, basta substituir o valor do tempo em qualquer uma das duas equações, resultando em $S = 800 \ m$.
$$\overline{AM} + \overline{ME} = 800 \ m \Rightarrow \overline{ME} = 120 \ m$$
Aplicando Pitágoras no triângulo $MCE$, obtemos que a hipotenusa é igual a $200 \ m$. Finalmente,
$$v = \dfrac{\overline{CE}}{40} = 5m/s$$
Escrevendo as equações da cinemática para cada uma das locomotivas, obtemos:
$$S_{A} = 1360 - 14t\\
S_{B} = 0 + 20t.$$
Como as locomotivas irão se encontrar, basta igualar a posição de ambos e encontrar o tempo em que tal evento ocorrerá.
$$1360 - 14t = 20t \Rightarrow t = 40 \ s$$
Para encontrar a posição de encontro, basta substituir o valor do tempo em qualquer uma das duas equações, resultando em $S = 800 \ m$.
$$\overline{AM} + \overline{ME} = 800 \ m \Rightarrow \overline{ME} = 120 \ m$$
Aplicando Pitágoras no triângulo $MCE$, obtemos que a hipotenusa é igual a $200 \ m$. Finalmente,
$$v = \dfrac{\overline{CE}}{40} = 5m/s$$

Ampliar Imagem




