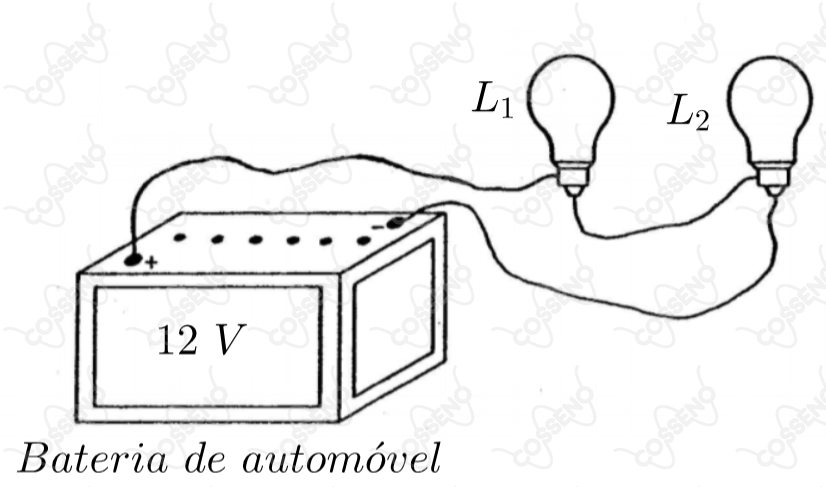
A figura a seguir mostra duas lâmpadas de automóvel fabricadas para funcionar em . As potências nominais (escritas nos bulbos das lâmpadas) são, respectivamente, e . Se elas forem ligadas, em série, conforme indica o desenho,
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Segundo enunciado, as lâmpadas foram fabricadas para trabalhar a $12 \ V$, sendo essa a tensão nominal das lâmpadas. Dessa forma, com conhecimento da potência nominal de cada lâmpada, podemos encontrar a resistência padrão de cada uma: \begin{matrix} Pot = { \dfrac{(\Delta V)^2}{R}} &\Rightarrow& R_1 = {{\dfrac{12^2}{5}}} \ \Omega &,& R_2 = {{\dfrac{6.12}{5}}} \ \Omega
\end{matrix}Nessa perspectiva, é sabido que as lâmpadas estão em série, logo, não é difícil encontrar a corrente que passa pelo sistema: \begin{matrix} \Delta V = (R_1 + R_2).i &\therefore& i = {{\dfrac{5}{18}}} \ A
\end{matrix}Por fim, a potência que cada uma está trabalhando: \begin{matrix} Pot = R.i^2 &\therefore& Pot_1 = {{\dfrac{20}{9}}} \ W&,& Pot_2 = {{\dfrac{10}{9}}} \ W
\end{matrix}Constata-se então que, a primeira lâmpada emite mais luz que a segunda. \begin{matrix} Letra \ (C)
\end{matrix}

