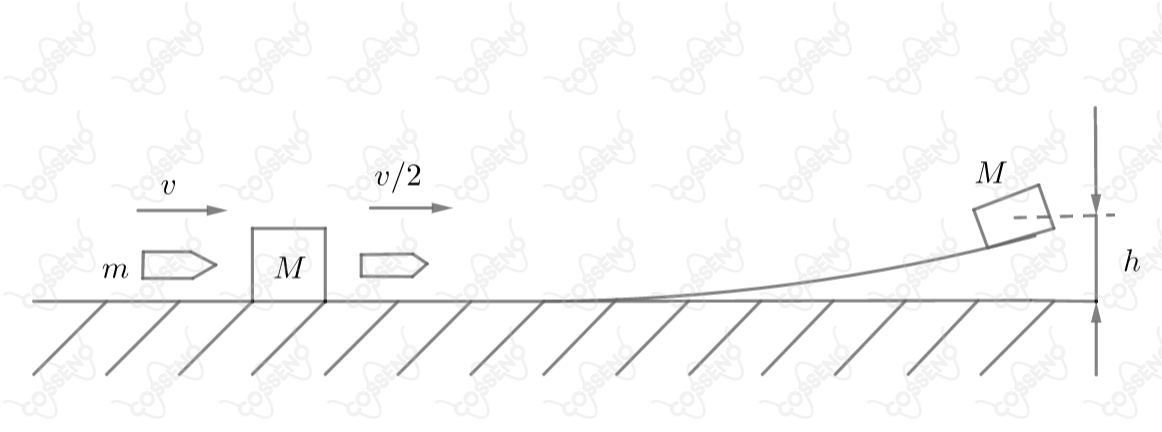
Um projétil de massa e velocidade atinge um objeto de massa , inicialmente imóvel. O projétil atravessa o corpo de massa e sai dele com velocidade . O corpo que foi atingido desliza por uma superfície sem atrito, subindo uma rampa até a altura . Nestas condições podemos afirmar que a velocidade inicial do projétil era de:
Conservação da Quantidade de Movimento ($u$ é a velocidade adquirida pelo bloco de massa $M$:
\begin{matrix} m.v + M.0 = m\cdot \dfrac{v}{2} + M.u & \Rightarrow & u = {{\dfrac{m.V}{2M}}} \ \ \ (1) \end{matrix}
Teorema do Trabalho Total (Adotando o solo como Nível de Referência)
\begin{matrix} Wtot = Wpeso = \Delta Ec & \Rightarrow& M.g.0 - M.g.h = {{\dfrac{M.0^2}{2}}} - {{\dfrac{M.u^2}{2}}} \ \ \ (2) \end{matrix}
Substituindo $(1)$ em $(2)$
\begin{matrix} v = {{\dfrac{2M}{m}}}\sqrt{2gh} \\ \\ Letra \ ( A ) \end{matrix}
$\color{red}{Adendo:}$ É possível usar a $Conservação \ de \ Energia \ Mecânica$ direto, porém, ela não é nada mais que um resultado do $Teorema \ do \ Trabalho \ Total$, fica ao seu critério o que preferir usar.
