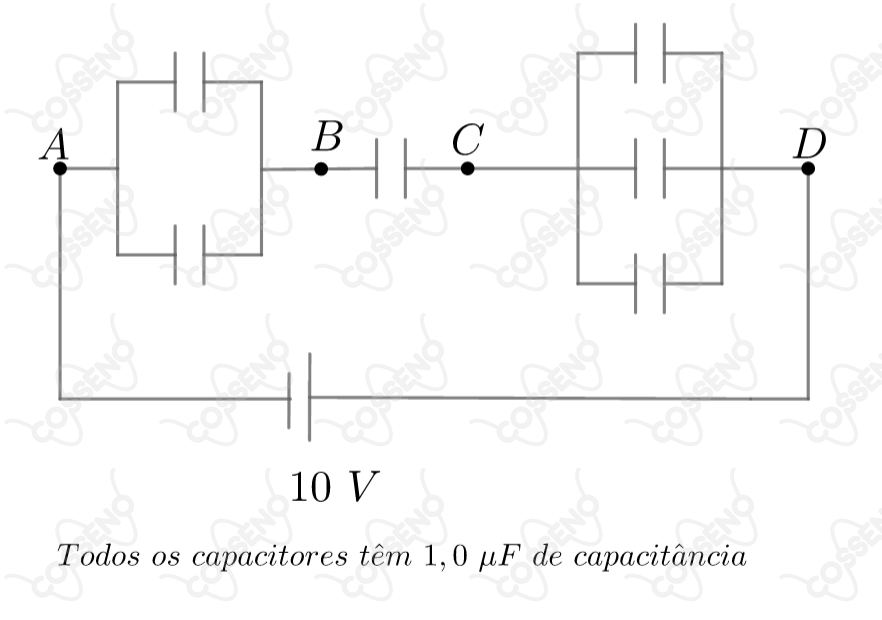
No arranjo de capacitores abaixo, onde todos eles têm de capacitância e os pontos A e D estão ligados a um gerador de pergunta-se: qual é a diferença de potencial entre os pontos B e C?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, dos capacitores em paralelo temos as equivalentes como somas, sendo assim, têm-se as capacitâncias $C_{AB} = 2 \ \mu \pu{F}$ , $C_{BC} = 1 \ \mu \pu{F}$ e $C_{CD} = 3 \ \mu \pu{F}$ , logo, com esses três em série, temos a equivalente $C_{AD}$ como: \begin{matrix} {\dfrac{1}{C_{AD}} = \dfrac{1}{C_{AB}} + \dfrac{1}{C_{BC}} + \dfrac{1}{C_{CD}}} &\Rightarrow& C_{AD} = \dfrac{6}{11} \ \mu \pu{F}
\end{matrix}Continuando, \begin{matrix} Q = C_{AD} \cdot \Delta V &\therefore& Q = \dfrac{60}{11} \ \pu{C}
\end{matrix}Atente que, esta carga $Q$ será a mesma em todos os capacitores, vide indução total, logo, para descobrirmos a $d.d.p$ entre os pontos $B$ e $C$, basta fazer: \begin{matrix} \Delta V_{AB} = {\dfrac{Q}{C_{CB}}} &\therefore& \fbox{$ \Delta V_{AB} \approx 5,4 \ V $}
\end{matrix} \begin{matrix} Letra \ (D)
\end{matrix}

