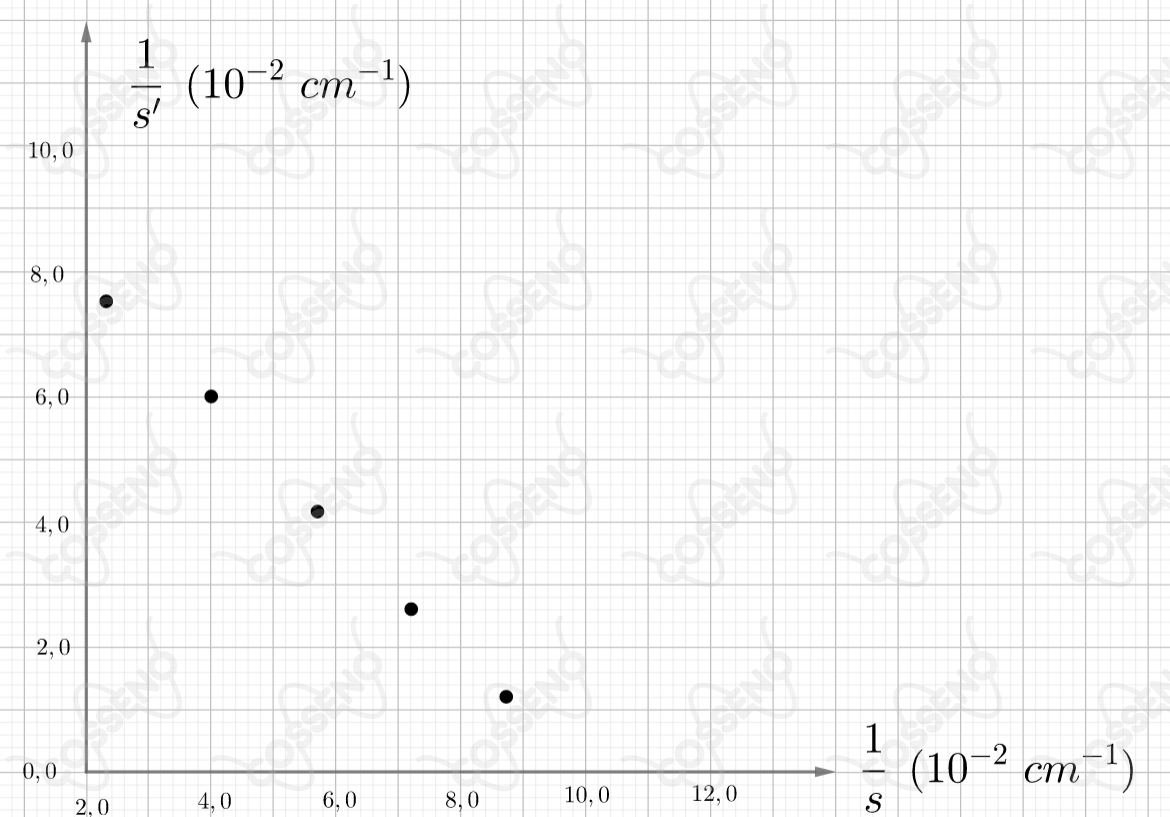
Numa certa experiência mediu-se a distância entre um objeto e uma lente e a distância s\,^\prime entre a lente e a sua imagem real, em vários pontos. O resultado dessas medições é apresentado na figura abaixo. Examinando-se cuidadosamente o gráfico concluiu-se que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ao supor válida a $\text{Equação de Gauss}$, temos: \begin{matrix} \Large{\frac{1}{f}} &=& \Large{\frac{1}{s}} &+& \Large{\frac{1}{s^{'}}}
\end{matrix} Em que, a situação do enunciado pode ser representada como: \begin{matrix}
(Objeto) &---(s)---& (Lente) &---(s^{'})---& (Imagem)
\end{matrix} Não é difícil perceber que há um ponto estratégico no gráfico, aquele o qual temos os resultados: \begin{matrix}
\frac{1}{s} = 4,0 &e& \frac{1}{s^{'}} = 6,0
\end{matrix} Assim, não é difícil inferir que: \begin{matrix} \fbox{$f = 10 \ cm$} \\ \\ Letra \ (A)
\end{matrix}

