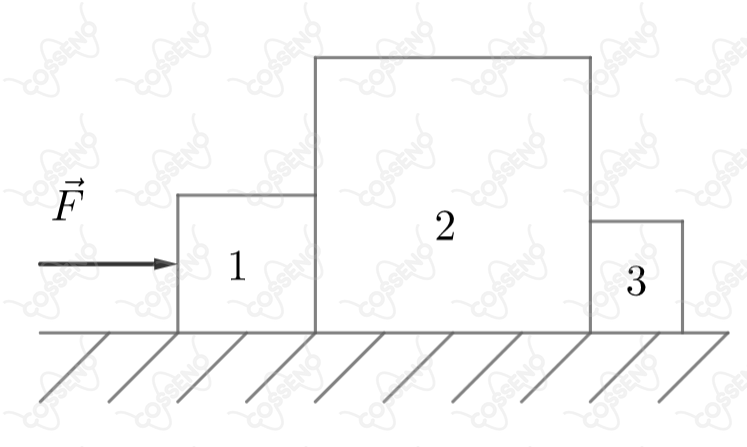
A figura abaixo representa três blocos de massas , e , respectivamente. Entre os blocos e o piso que os apoia existe atrito, cujos coeficientes cinético e estático são, respectivamente, e , e a aceleração da gravidade vale . Se ao bloco for aplicada uma força horizontal de , pode-se afirmar que a força que bloco 2 aplica sobre o bloco 3 vale:
Analisando se há movimento em todo conjunto - condição para que $3$ se mova - podemos admitir um corpo de massa $m = m_1 + m_2 + m_3$, em que para se ter movimento $F\ge fat_e$, vejamos: \begin{matrix} fat_e \le 0,15 \cdot (40) = 6 \ \pu{N} &\therefore& F > fat_e &\because& F = 10 \ \pu{N}
\end{matrix}$\color{orangered}{Obs:}$ $fat_e: \ \text{Força de atrito estático}$
Sabido que há movimento, pode-se encontrar a aceleração com que o conjunto se desloca, essa aceleração será a mesma para cada bloco. Atente que o atrito agora é cinético:\begin{matrix} (m_1 + m_2 + m_3) \cdot a = F - fat_c &\Rightarrow& 4 \cdot a = 10 - 0,1\cdot (40) &\therefore& a= 1,5 \ \pu{m/s-2}
\end{matrix}$\color{orangered}{Obs:}$ $fat_c: \ \text{Força de atrito cinético}$
Analisando as forças que atuam no bloco $3$, vamos chamar a força que o bloco $2$ faz em $3$ de $F_{2(3)}$, então: \begin{matrix}m_3 \cdot a = F_{2(3)} - fat_3 &\Rightarrow&
(0,5) \cdot (1,5) = F_{2(3)} - 0,1 \cdot (5) &\therefore& F_{2(3)} = 1,25 \ \pu{N} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
