O coeficiente médio de dilatação térmica linear do aço é . Usando trilhos de aço de de comprimento um engenheiro construiu uma ferrovia deixando um espaço de entre os trilhos, quando a temperatura era de . Num dia de sol forte os trilhos soltaram-se dos dormentes. Qual dos valores abaixo corresponde à mínima temperatura que deve ter sido atingida pelo trilhos ?
A máxima temperatura que os trilhos podem suportar sem se soltar é aquela a qual a dilatação será exatamente o espaço entre os trilhos, assim, temos a mínima temperatura para os trilhos se tocarem. Com isso, têm-se para dilatação linear: \begin{matrix} \Delta L = L_o\cdot \alpha \cdot \Delta \theta \\ \\ 0,5 \cdot 10^{-2} = 8,0 \cdot 1,2.10^{-5} \cdot (T-28) \\ \\ \fbox{$T = 80^{\circ}C$}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Não se esqueça de converter o espaço entre os trilhos para metro $\pu{(m)}$.
21:37 22/02/2023
Oi boa tarde, alguém sabe o porque o 0,5 é multiplicado por 10^^−2?
23:12 16/03/2023
Cara é como sugere o Obs, 0,5 tá em centímetro ai pra passar pra metro multiplica por 10^-2=1/100
02:50 21/03/2023
Olá, Fernando! Multiplicar por 10^-2 é dividir por 100, ou seja, ele converteu de cm para metros. Bons estudos!
Vou deixar este comentário para caso alguém tenha a seguinte dúvida: por que devo considerar o $\Delta L = 0,5 \cdot 10^{-2} \ m$ como colocou o ITA IIT ao invés de $0,25 \cdot 10^{-2} \ m$?
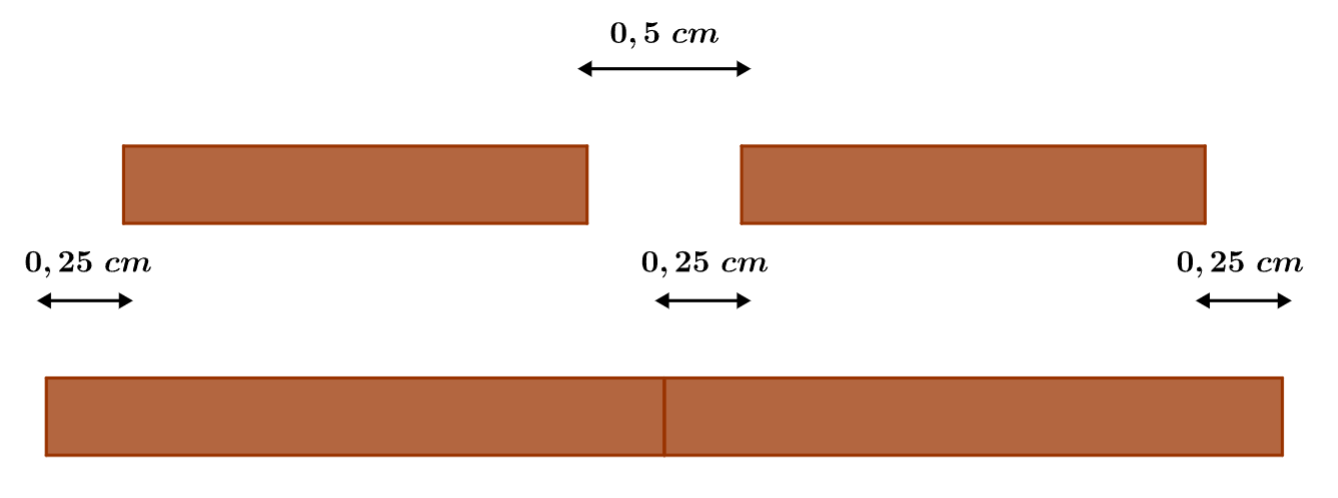
Isso acontece, pois na verdade o trilho irá dilatar em ambos os lados, tanto na direita, quanto na esquerda, lembre-se que temos trilhos ao lado de trilhos, então teremos sim a dilatação de $0,25 \cdot 10^{-2}$, no entanto, teremos essa dilatação na esquerda e na direita, por isso a variação deve ser $0,5 \cdot 10^{-2}.$ Veja na figura abaixo, nela temos em cima a situação inicial e logo abaixo a situação após a dilatação com os trilhos se encostando.
Ampliar Imagem
