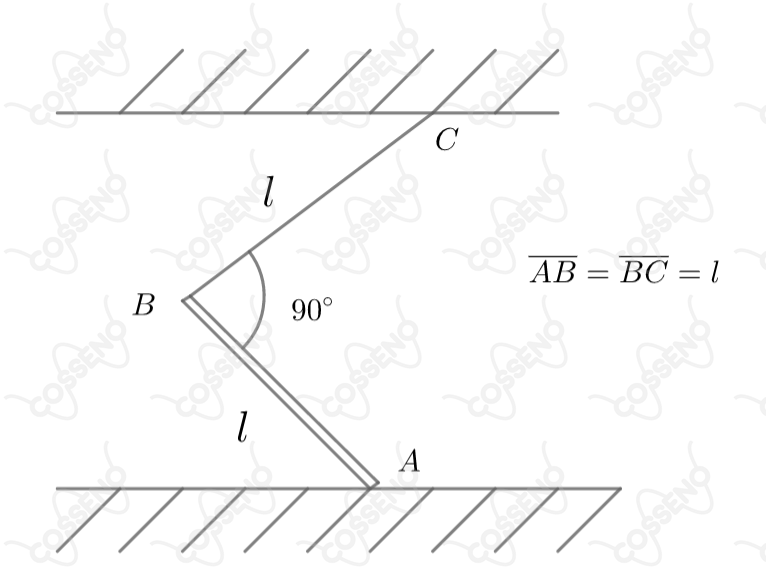
Para que a haste homogênea de peso permaneça em equilíbrio suportada pelo fio , a força de atrito em deve ser:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Estando o sistema em equilíbrio, a soma vetorial das forças assim como a soma vetorial dos momentos de força
devem ser iguais a $0$.
Na haste atuam a tração exercida pelo fio $(T)$, o peso da haste $(P)$, o atrito com a superfície $(F_{at})$ e a força normal $(F_n)$.
Decompondo $T$ vemos que $Ty=Tx=T\cdot\sin 45°$
Verticalmente temos $P$, $T_x$ e $F_n$:
$T_x+N=P$
Horizontalmente temos $T_y$ e $Fat$;$$F_{at}=T_y=T\cdot\sin 45°$$
Teremos momentos de força em $P$ e em $T$, sendo $P$ em sentido anti-horário e $T$ em sentido anti-horário, $M_p=M_t$ para termos o sistema em equilíbrio.
$M_p=P\cdot\frac{l}{2}\cdot\sin 45°$
Sendo $\frac{l}{2}$ a distância entre o eixo de rotação e o ponto de aplicação da força peso e $45°$ o ângulo formado entre o braço de alavanca e o peso$$M_t=T\cdot l\cdot \sin 90°$$
Sendo $l$ a distância entre o eixo de rotação e o ponto de aplicação da tração e $90°$ o ângulo formado entre o braço de alavanca e a tração
$$M_t=M_p \\ P\cdot\frac{l}{2}\cdot\sin 45°=T\cdot l\cdot \sin 90°\\ \frac{P\cdot\sin 45°}{2}=T$$
Substituindo em $F_{at}=T\cdot\sin 45°$ teremos: $$F_{at}=\frac{P\cdot\sin 45°}{2}\cdot\sin 45°\\ F_{at}=\frac{P\cdot\left(\frac{\sqrt{2}}{2}\right)^2}{2} \\ F_{at}=\frac{P\cdot\frac{2}{4}}{2}\\ F_{at}=\frac{2P}{8}\\ F_{at}=\frac{P}{4} \Longrightarrow\boxed{\text{Alternativa A)}}$$

