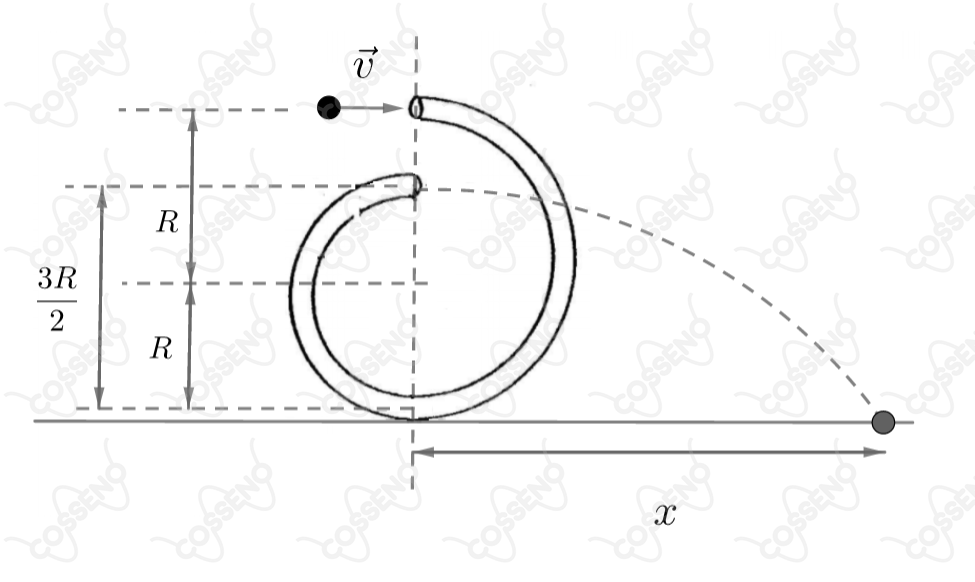
Uma pequena esfera penetra com velocidade em um tubo oco, recurvado, colocado num plano vertical, como mostra a figura, num local onde a aceleração da gravidade é . Supondo que a esfera percorra a região interior ao tubo sem atrito e acabe saindo horizontalmente pela extremidade, pergunta-se: que distância, , horizontal, ela percorrerá até tocar o solo?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Admitindo um sistema conservativo, denotemos o módulo da velocidade com que a esfera sai do tubo de $u$, assim, têm-se: \begin{matrix} \Delta E_M = 0 &\Rightarrow&
mg(2R) + {\large{\frac{mu^2}{2}}} - mg({\large{\frac{3R}{2}}}) - {\large{\frac{mv^2}{2}}} = 0 &\therefore& u = \sqrt{v^2 + gR}
\end{matrix}No momento em que a esfera sai do tubo ela cai num movimento retilíneo uniformemente acelerado, conhecida sua lei horária, podemos descobrir seu tempo de queda, veja: \begin{matrix} \Delta y =u_y \Delta t + a {\large{\frac{\Delta t^2}{2}}} &,& a = -g &\wedge& u_y = 0 &\wedge& \Delta y = - {\large{\frac{3R}{2}}} &\therefore& \Delta t = \sqrt{{\large{\frac{3R}{g}}}}
\end{matrix}Conhecido o tempo de queda, e sabido que a esfera realiza um movimento uniforme na horizontal, a distância que ela percorrerá até atingir o solo será:\begin{matrix} x = u_x \Delta t &,& u_x = u &\therefore& x = \sqrt{{\large{\frac{3R}{g}}} (v^2 + gR)} & \tiny{\blacksquare}
\end{matrix}\begin{matrix} Letra \ (D)
\end{matrix}
Seja $A$ o ponto de entrada da esfera ao tubo e $B$ o ponto de saída. Perceba que como não existe atrito no tubo , a energia mecânica se conserva do ponto $A$ ao ponto $B$ , logo , podemos escrever a seguinte equação :
$E_{M_{A}} = E_{M_{B}}$
$E_{c_{A}} + E_{p_{A}} = E_{c_{B}} + E_{p_{B}} $
$\dfrac{m \cdot (v_{a})^2}{2} + m\cdot g \cdot 2R = \dfrac{m \cdot (v_{b})^2}{2}+ m\cdot g \cdot \dfrac{3R}{2} $
$ \implies (v_{a})^2 + 4Rg = (v_{b})^2 + 3Rg$
$\implies (v_{b})^2 = (v_{a})^2 + Rg \implies v_{b} = \sqrt{v_{a}^2 + Rg} =\sqrt{v^2 + Rg} $
A partir do ponto $B$ a esfera começa a percorrer um movimento oblíquo. Analisando o movimento horizontal dessa esfera , podemos concluir que $ x = (v_{b} \cdot t_{des})$ onde $t_{des}$ é o tempo de decida da esfera.
Agora vamos analisar o movimento da esfera na vertical , imagine que essa esfera estivesse em um movimento de subida com uma velocidade inicial $v_{0}$ , sabemos que em um movimento de subida temos que $ v_{y} = v_{0} - g \cdot t \therefore g \cdot t_{sub} = v_{0} \implies t_{sub} = \dfrac{v_{0}}{g} $ e que $ (v_{y})^2 = (v_{0})^2 - 2\cdot g \cdot H \implies 2 \cdot g \cdot H_{max} = (v_{0})^2 \implies v_{0} = \sqrt{ 2 \cdot g \cdot H_{max} } \therefore t_{sub} = \dfrac{ \sqrt{ 2 \cdot g \cdot H_{max} }}{g} = t_{sub} = \sqrt{ \dfrac{2 \cdot H_{max}}{g}}$ onde $ t_{sub} $ é o tempo de subida. Como o tempo de subida é igual o tempo de decida e sendo $H_{max} = \dfrac{3R}{2}$ a altura máxima alcançada pela esfera , portanto :
$ x = (v_{b} \cdot t_{des}) = (v_{b} \cdot t_{sub}) = (\sqrt{v^2 + Rg} \cdot \sqrt{ \dfrac{2 \cdot \dfrac{3R}{2}}{g}}) = (\sqrt{v^2 + Rg} \cdot \sqrt{ \dfrac{3R}{g}})$
$= x = \sqrt{\dfrac{3R}{g} \cdot (v^2 + gR)} $
$\textbf{Resposta : Letra (D)}$


