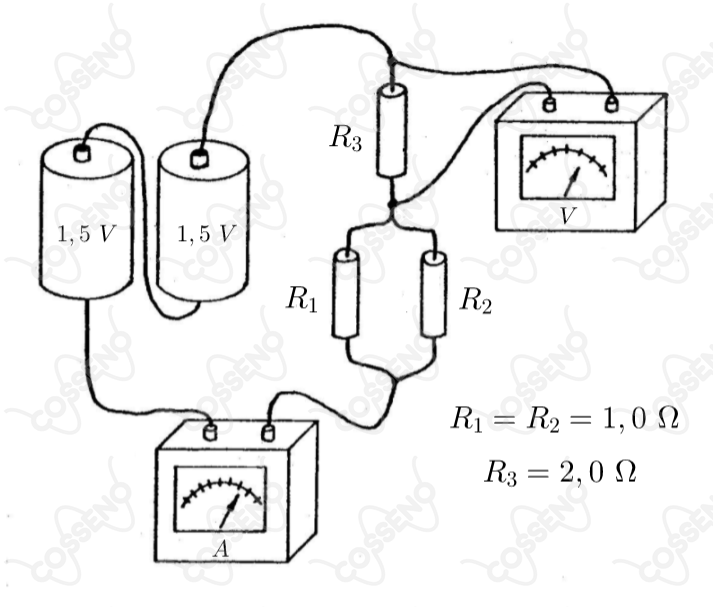
No circuito desenhado abaixo, têm-se duas pilhas de cada, de resistências internas desprezíveis, ligadas em série, fornecendo corrente para três resistores com os valores indicados. Ao circuito estão ligados ainda um voltímetro e um amperímetro de resistências internas, respectivamente, muito alta e muito baixa. As leituras desses instrumentos são, respectivamente:
Podemos redesenhar o sistema, mas antes, repare que há uma associação de geradores em série, façamos então um equivalente, este que será $\epsilon = 3V$. Assim, veja a figura abaixo:
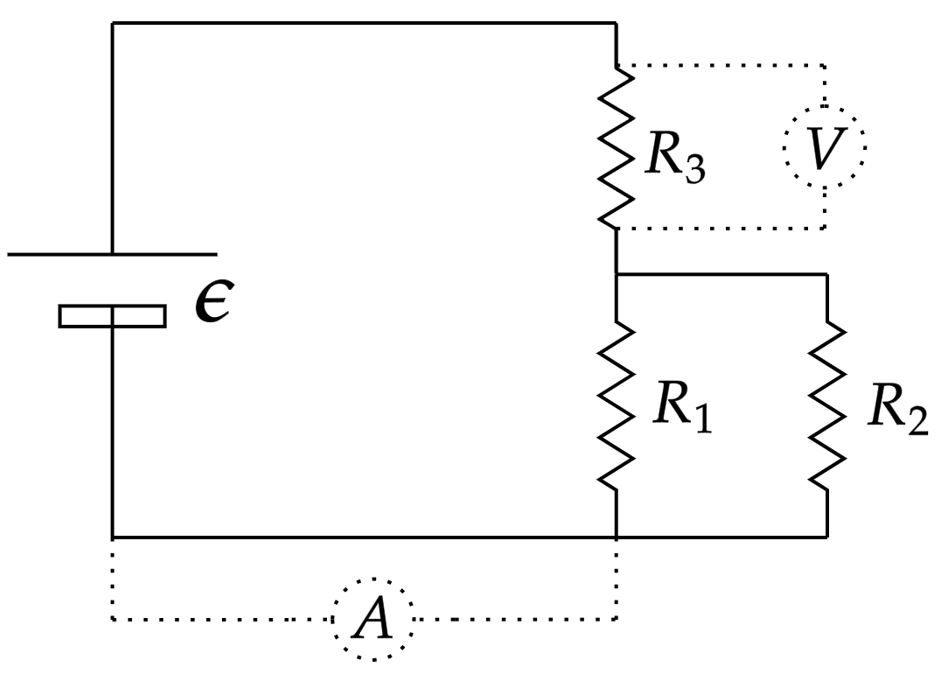Começando pela corrente que passa pelo amperímetro, precisamos encontrar a resistência equivalente $(R_e)$ do sistema, ela será: \begin{matrix} R_e = R_3 + {\dfrac{R_1.R_2}{R_1 + R_2}} &\Rightarrow& R_e = 2,5 \ \Omega
\end{matrix}$\text{Primeira Lei de Ohm}$: \begin{matrix} \epsilon = R_e.i &\Rightarrow& \fbox{$i = 1,2 \ A$}
\end{matrix}Agora, com conhecimento da intensidade da corrente, não é difícil encontrar a $d.d.p$ que passa no voltímetro, denotemos ela de $\Delta V$, sendo assim: \begin{matrix} \Delta V = R_3.i &\Rightarrow& \fbox{$\Delta V = 2,4 \ V$}
\end{matrix} \begin{matrix} Letra \ (D)
\end{matrix}
Ampliar Imagem
