Um corpo em movimento retilíneo tem a sua velocidade em função do tempo dada pelo gráfico abaixo:
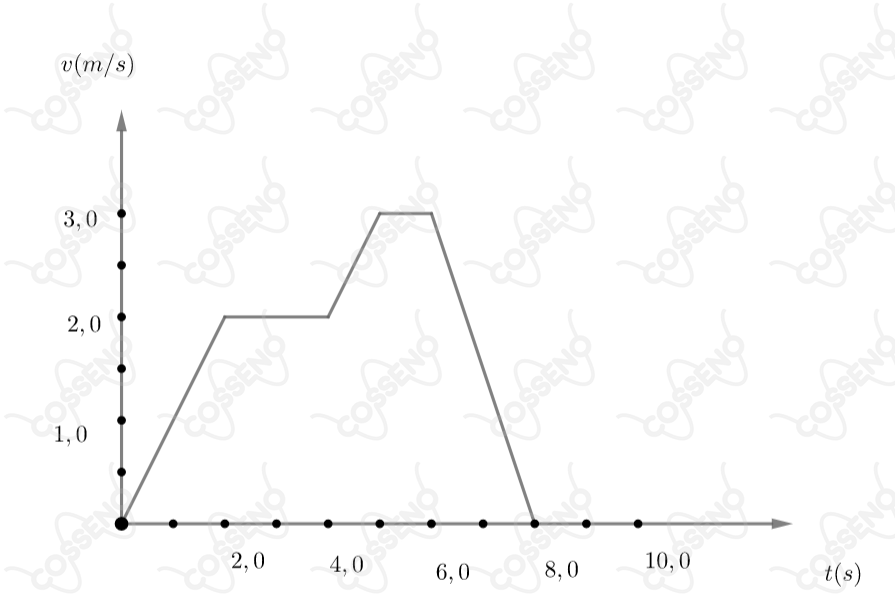
Neste caso pode-se afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Sabendo que a área do gráfico é numericamente igual ao deslocamento, analisemos as alternativas:
$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Falsa}}$
Calculando a área do gráfico de $t=4s$ até $t=8s$:
\begin{matrix} \Delta S_1 = (2,5 + 3 + 3) = 8,5 \ \pu{m} \\ \\
V_1 = \dfrac{\Delta S_1}{\Delta T_1} = \dfrac{8,5}{4} \ne 2 \ \pu{m/s}
\end{matrix}
$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Falsa}}$
\begin{matrix} \Delta S_2 = \dfrac{(4 + 2).2}{2} = 6 \ \pu{m} \ne 10 \ \pu{m} \\ \\
\end{matrix}
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Falsa}}$
Calculando a aceleração entre $t=0s$ até $t=2s$
\begin{matrix} a_3 = \dfrac{\Delta V_3}{\Delta T_3} = \dfrac{2-0}{2-0} = 1 \ \pu{m/s^2} \\ \\ F(r) = m \cdot a = 2\cdot 1 = 2 \ \pu{N} \ne 0,5 \ \pu{N}
\end{matrix}
$• \ \text{Alternativa (D):}$ $\color{orangered}{\text{Falsa}}$
Calculando a aceleração entre $t=0s$ até $t=8s$
\begin{matrix} a_4 = \dfrac{\Delta V_4}{\Delta T_4} = \dfrac{0-0}{8-0} = 0 \ \pu{m/s^2} \ne 2 \ \pu{m/s^2}
\end{matrix}
$• \ \text{Alternativa (E):}$ $\color{royalblue}{\text{Verdadeira}}$
Realmente, está tudo errado.
\begin{matrix} Letra \ (E)
\end{matrix}

