Veja que, as duas primeiras desigualdades nos dão linhas retas em suas igualdades, ajeitando ambas, encontramos as inequações paramétricas. Além disso, o disco fornecido pelo enunciado também pode ser melhor representado, dele sabemos o centro $C = (1,0)$ do disco, e seu raio $r = \sqrt{2}$ : \begin{matrix} y \ge x - 1 &,& y \ge 1 - x &,& (x-1)^2 + (y - 0)^2 \le (\sqrt{2})^2 \end{matrix} $\color{orange}{Nota:}$ Constate o coeficiente angular das pseudo-retas, elas são perpendiculares. A intersecção de ambas as desigualdades num plano coordenado: 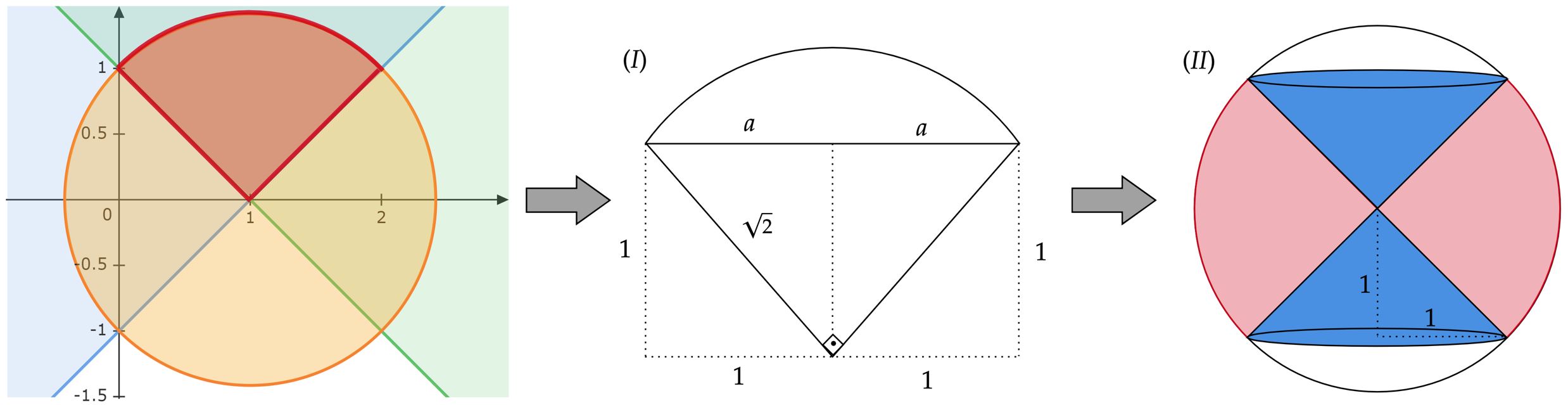$\color{royalblue}{Adendo:}$ Na figura $(II)$ há uma rotação de $90^{\circ}$para melhor visualização. Repare que, a intersecção nos apresenta um setor circular, desse modo, ao fazer a rotação em torno do eixo $x$ encontramos um setor esférico. Atente que, existem várias formas de se calcular este volume, o mais direto (creio eu), seria partir para equação do setor esférico: \begin{matrix}S_e = \dfrac{2}{3} \cdot \pi \cdot r^2 \cdot (2a) \end{matrix} Não é difícil encontrar $2a$, repare na imagem acima em $(I)$: \begin{matrix} a = 1 &\Rightarrow& \fbox{$ S_e =\dfrac{8}{3} \cdot \pi $} \end{matrix} \begin{matrix} Letra \ (B) \end{matrix} $\color{orangered}{Obs:}$ Como dito anteriormente, há outras formas de calcular o volume do setor esférico, você poderia partir do volume da zona esférica e remover os dois cones como na figura $(II)$. Noutro prisma, você poderia partir da esfera, remover as duas calotas e os mesmos dois cones.