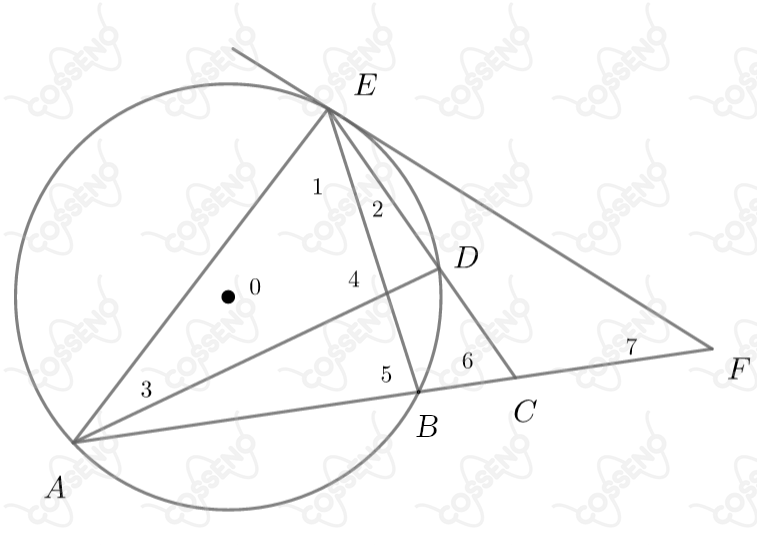
Na figura abaixo é o centro de uma circunferência. Sabendo-se que a reta que passa por e é tangente a esta circunferência e que a medida dos ângulos , e são dadas, respectivamente, por , , , determinar a medida dos ângulos , , e . Nas alternativas abaixo considere os valores dados iguais às medidas de , , e , respectivamente.
CossenoGPT
Teste gratuitamente agora mesmo! 

Ângulo $ \hat{4}$:\begin{matrix} 180º =\hat{1} + \hat{3} + \hat{4} &\Rightarrow& \fbox{$\hat{4} = 97º$}
\end{matrix}Ângulo $ \hat{5}$:
Perceba que, pelo $\text{Arco Capaz}$ o ângulo $ \hat{2}$ é congruente ao ângulo $D \hat{A} C$, assim: \begin{matrix} 180º = \hat{1} + (\hat{3} + D\hat{A}C) + \hat{5} &\Rightarrow& \fbox{$\hat{5} = 79º$}
\end{matrix}Ângulo $ \hat{6}$:\begin{matrix} 180º = (\hat{1} + \hat{2})+ (\hat{3} + D\hat{A}C) + \hat{6} &\Rightarrow& \fbox{$\hat{6} = 61º$}
\end{matrix}Ângulo $ \hat{7}$:
Veja que, o $ \hat{7}$ é um ângulo $\text{Excêntrico Exteriror}$, além disso, $(\hat{3} + D\hat{A}C) $ e $\hat{5} $ são $\text{ângulos inscritos}$, isto é, seus respectivos arcos (ângulos centrais) representam o dobro de seus ângulos. Dessa forma, temos:\begin{matrix} (\hat{3} + D\hat{A}C) = 52º & \Rightarrow & \overset{\frown}{EB} = 2\cdot 52º \\ \hat{5} = 79º & \Rightarrow & \overset{\frown}{AE} = 2\cdot 79º
\end{matrix}Portanto,\begin{matrix} \hat{7} = {{\dfrac{\overset{\frown}{AE} \ - \ \overset{\frown}{EB} }{2}}} &\therefore& \fbox{$\hat{7} = 27º$}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

