Segundo informações do enunciado, têm-se uma figura como: 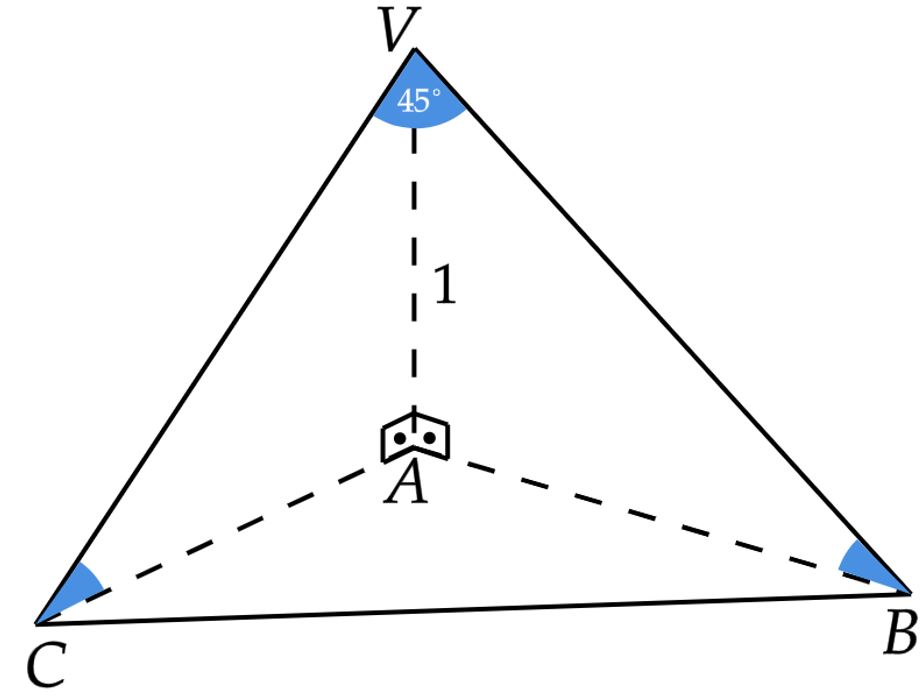Analisando os triângulos $AVB$ e $AVC$, pelo ângulo das faces laterais, têm-se: \begin{matrix} \tan{45^{\circ}} = {{\dfrac{\overline{AC}}{1}}} = {{\dfrac{\overline{AB}}{1}}} &\Rightarrow& \overline{AC} = \overline{AB} = 1 \ u.m &\therefore& \overline{VC} = \overline{VB} = \sqrt{2 } \ \ u.m \end{matrix}Continuando, visto o triângulo $VBC$, ao aplicar a $\text{Lei dos Cossenos}$ se constata: \begin{matrix} (\overline{CB})^2 = (\overline{VC})^2 + (\overline{VB})^2 - 2.(\overline{VC}).(\overline{VB}).\cos{45^{\circ}} &\therefore& \overline{CB} = \sqrt{2 (2 - \sqrt{2})} \ \ u.m \end{matrix}Adiante, note que o triângulo da base $ABC$ é isósceles, assim, pode-se dividir sua área em dois triângulos retângulos de hipotenusas $\overline{AC}$ e $\overline{AB}$, com mesmo cateto $y$, então: \begin{matrix} (\overline{AC})^2 = {{ \left( \dfrac{\overline{CB}}{2} \right)^2}} + y^2 &\therefore& y = {{ \sqrt{\dfrac{\sqrt{2}}{2} }} }& u.m \end{matrix}A área do triângulo $ABC$: \begin{matrix} [ABC] = 2 \cdot {{\dfrac{{{ \left( \dfrac{\overline{CB}}{2} \right)}} \cdot y}{2}}} =2 \cdot {{ \left(\dfrac{\dfrac{\sqrt{2 (2 - \sqrt{2})}}{2} \cdot {{ \sqrt{\dfrac{\sqrt{2}}{2} }} }}{2} \right)}} &\therefore& [ABC] = {{\dfrac{\sqrt{(2\sqrt{2} - 2 )}}{2}}} \ \ u.a \end{matrix}Por fim, o volume da pirâmide: \begin{matrix} V = {{\dfrac{\overline{VA}}{3}}} \cdot [ABC] &\therefore& V = {{\dfrac{1}{6}}} \cdot \sqrt{(2\sqrt{2} - 2 )} \ \ u.v & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (A) \end{matrix}