Duas molas ideais, sem massa e de constantes de elasticidade e k_1<k_2$ acham-se dependuradas no teto de uma sala. Em suas extremidades livres penduram-se massas idênticas.
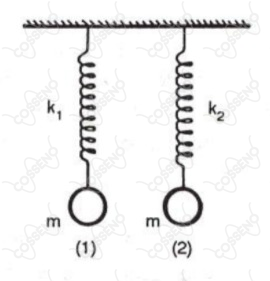
Observa-se que, quando os sistemas oscilam verticalmente, as massas atingem a mesma velocidade máxima. Indicando por A1 e A2 as amplitudes dos movimentos e por E1 e E2 as energias mecânicas dos sistemas (1) e (2), respectivamente, podemos dizer que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Gabarito que acredito fortemente: B
V1 = V2
A1w1 = A2w2
A1(k1/m)^½=A2(k2/m)^½
A1/A2=(k1/k2)^½ < 1
A1 < A2
E = kA²/2
E1 = [k1(A1)^½]/2
da relação das velocidades:
E1 = E2
Se a constante elástica do sistema 1 é menor que a constante elástica do sistema 2, então a amplitude de movimento do sistema 1 deve ser maior que a amplitude do sistema 2. Você pode pensar nisso por duas maneiras:
$1)$ Vendo que a constante elástica é como se fosse uma força de atrito que dificulta o movimento.; ou
$2)$ Pode verificar a partir do equilíbrio do sistema, isto é,
$$k_{1}A_{1} = mg,$$
em que o fato de $k_{1}$ diminuir, implica no aumento de $A_{1}$, pois são inversamente proporcionais. Pensando a respeito da energia, você pode tentar forçar aparecer o termo da energia mecânica nos dois casos multiplicando pelas suas amplitudes e dividindo por 2, nisso teremos uma constante multiplica pela amplitude e como a amplitude do primeiro sistema é maior que a amplitude do segundo sistema, então a energia mecânica do sistema 1 também será maior que a energia do sistema 2.


