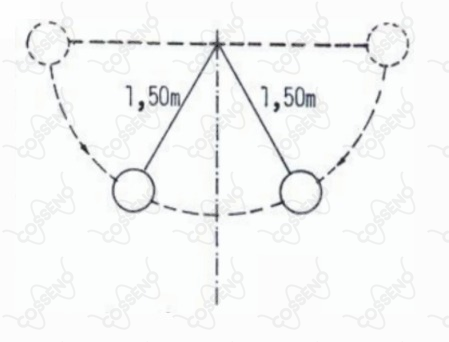
Dois corpos feitos de chumbo estão suspensos a um mesmo ponto por fios de comprimentos iguais a . Esticam-se os dois ao longo de uma mesma horizontal e em seguida, abandonam-se os corpos, de forma que eles se chocam e ficam em repouso, Desprezando as perdas mecânicas e admitindo que toda a energia se transforma em calor e sabendo que o calor especifico do chumbo é e a aceleração da gravidade de , podemos afirmar que a elevação de temperatura dos corpos é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, como os corpos ficam em repouso após o choque, têm-se que os corpos convertem toda energia potencial em energia térmica. No caso, visto que os corpos são os mesmos, assim como ambos partem de situações idênticas - mesma altura e em repouso -, têm-se que as energias e conversões são iguais, ou seja, para qualquer um dos corpos:\begin{matrix}
E_{potencial} = Q
\end{matrix}Pensando na situação inicial, há apenas energia potencial gravitacional, e toda ela será convertida em energia térmica. Assim, com conhecimento da equação fundamental da calorimetria,\begin{matrix}
mgh = mc\Delta T
\end{matrix}Observe que ambas as massas $m$ devem estar na mesma unidade de medida, à esquerda da equação temos a massa em quilos, consequentemente, à direita devemos ter o mesmo. Por isso, deve-se atentar a ao calor específico do chumbo, este que está em gramas, ou seja, é necessário converte-lo para quilos, o que não é difícil, veja:\begin{matrix}
c = \dfrac{0,130 \ \pu{J ºC^{-1}}}{1\ \pu{g}} \cdot \dfrac{1000 \ \pu{g}}{1 \ \pu{kg}} &\therefore& c = 130 \ \pu{J/kgºC }
\end{matrix}Com isso, \begin{matrix}
9,8 \cdot 1,5 = 130 \cdot \Delta T &\therefore& \Delta T = 0,113 \ \pu{ºC }
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

