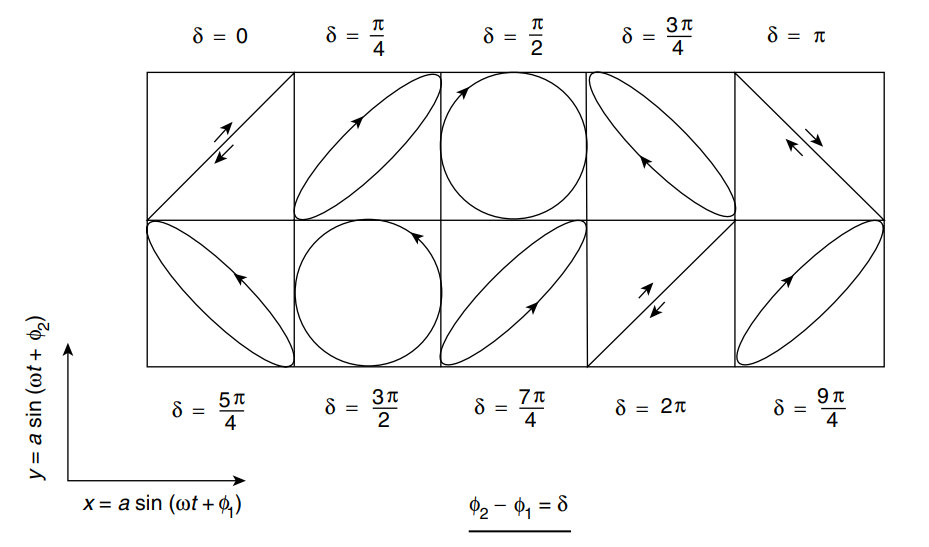
Na figura ao lado, que representa a combinação de dois movimentos harmônicos simples em eixos perpendiculares e , sendo um número positivo, qual das expressões abaixo poderá representá-lo?

CossenoGPT
Teste
gratuitamente agora
mesmo! 

Vamos pensar no que acontece com diferentes valores de $\alpha$.
Começando com $\alpha=0$, a combinação dos movimentos harmônicos simples $(x,y)=(A\sin\omega t, B\sin\omega t)$ formará um percurso reto linear (coincide com parte do gráfico de $y=Bx/A$) atravessando os quadrantes $1$ e $3$, dado que $A,B\in\mathbb{R}^+$.
Já com $\alpha=90º$, a combinação será $$(x,y)=(A\sin\omega t, B\sin(\omega t + 90º))\\ (x,y)=(A\sin\omega t, B\cos\omega t)$$ que corresponde à equação paramétrica de uma elipse, de modo que seu eixo maior atravesse os quadrantes $1$ e $3$ pois $A,B\in\mathbb{R}^+$. Note que, para $A=B$, teríamos um círculo.
Assim, para valores intermediários, $0<\alpha<90º$ pense na linha com uma dimensão "expandindo", correspondente ao eixo menor da elipse.
Já para valores $\alpha>90º$, note que $y=B\sin(\omega t + \alpha)$ vai decrescendo em relação ao valor quando $\alpha=90º$, fazendo com que a inclinação da elipse seja para a esquerda: o eixo maior agora cruza os quadrantes $2$ e $4$. Até que, quando $\alpha=180º$, a elipse degenera novamente para uma reta, mas desta vez passando pelos quadrantes $2$ e $4$: $(y=-Bx/A)$.
Portanto, a única alternativa válida que sobrou no gabarito foi $\boxed{\text{B: }\alpha\in(0,90º)}$, dado que vemos uma elipse de eixo maior atravessando os eixos $1$ e $3$.
 Crédito da imagem: Universitas PGRI Palembang, Indonésia
Chamamos essas figuras de curvas de Lissajous, aqui para valores de frequências iguais (é um caso especial).
Recomendo ler mais sobre o tema a título de curiosidade!
Qualquer coisa é só perguntar aqui embaixo nos comentários, bons estudos! 🚀
Crédito da imagem: Universitas PGRI Palembang, Indonésia
Chamamos essas figuras de curvas de Lissajous, aqui para valores de frequências iguais (é um caso especial).
Recomendo ler mais sobre o tema a título de curiosidade!
Qualquer coisa é só perguntar aqui embaixo nos comentários, bons estudos! 🚀

Ampliar Imagem
Deixando um pequeno complemento.
Sabe-se pelo enunciado que
$$x = A\sin (\omega t) \ , \ y = B\sin(\omega t + \alpha).$$
Pela equação fundamental da trigonometria, pode-se escrever que
$$\dfrac{x^{2}}{A^{2}} + \cos^{2} (\omega t) = 1 \Rightarrow \cos (\omega t) = \dfrac{\sqrt{A^{2} - x^{2}}}{A}.$$
Abrindo agora a equação de $y$, iremos obter
$$y = B(\sin (\omega t) \cos \alpha + \cos (\omega t) \sin \alpha) \Rightarrow \dfrac{y}{B} = \dfrac{x}{A}\cos \alpha + \dfrac{\sqrt{A^{2} - x^{2}}}{A} \sin \alpha \Rightarrow$$
$$\Rightarrow Ay - xB\cos \alpha = B\sqrt{A^{2} - x^{2}}\sin \alpha \Rightarrow B^{2}\sin^{2} \alpha(A^{2} - x^{2}) = A^{2}y^{2} - 2AyxB\cos \alpha + x^{2}B^{2}\cos^{2} \alpha \Rightarrow$$
$$\Rightarrow A^{2}B^{2}\sin^{2} \alpha = x^{2}B^{2}(\cos^{2} \alpha + \sin^{2} \alpha) + A^{2}y^{2} - 2AyxB\cos \alpha \Rightarrow$$
$$\Rightarrow \boxed{\sin^{2} \alpha = \dfrac{x^{2}}{A^{2}} + \dfrac{y^{2}}{B^{2}} - \dfrac{2yx\cos \alpha}{AB}}$$
Então, quando o prof. Nicholas disse que $\alpha = 90^\circ$, por exemplo, basta substituir na fórmula acima que iremos obter que
$$1 = \dfrac{x^{2}}{A^{2}} + \dfrac{y^{2}}{B^{2}}$$
Que é justamente a equação da elipse que já conhecemos!

23:14 18/07/2023
Perfeito! É uma saída mais algébrica para resolver o problema, chegando no termo geral da elipse rotacionada 🚀


