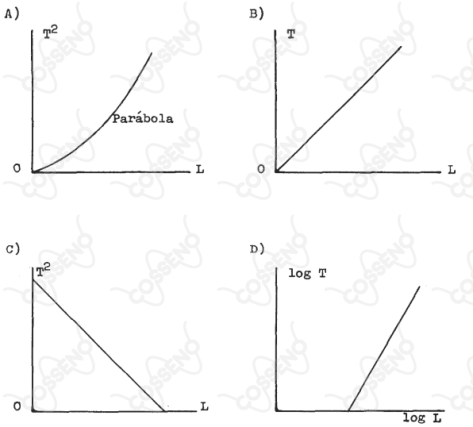
O período de um pêndulo simples é dado pela seguinte expressão:onde é o comprimento do pêndulo e é a aceleração da gravidade local. Qual dos gráficos abaixo representa essa lei?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

O bizu para questões de gráficos como esse é isolar a componente vertical e analisar o que é pedido.
$a) \ \text{e} \ c)$ Veja que nessas alternativas temos o período ao quadrado, então vamos buscar essa informação.
$$T^{2} = 4\pi^{2} \cdot \dfrac{L}{g} \Rightarrow T^{2} = k \cdot L,$$
em que $k = \frac{4\pi^{2}}{g}.$ Veja que pela expressão acima, temos uma uma função que depende do parâmetro $L$ que é linear, logo não pode ser a letra A por ser uma parábola e nem a letra C, pois a função deveria ser crescente, o que faz bastante sentido, pois se o comprimento do fio for maior, a amplitude também será e irá demorar mais tempo para que uma oscilação completa ocorra.
$b)$ Essa alternativa também não é verdade, pois é dito que a $T$ é uma função do primeiro grau que depende de $L$, o que é incorreto, pois deveria ser $T^{2}$ conforme as alternativas anteriores. Isso também poderia ser visto vendo que $T = k' \cdot L^{\frac{1}{2}}$ o que não caracteriza uma função do primeiro grau.
$d)$ Vamos tentar tirar o log da expressão dada pelo enunciado.
$$\log T = \log (2\pi) + \log \left(\dfrac{L}{g}\right)^{\frac{1}{2}} = \log (2) + \log (\pi) + \dfrac{1}{2}\log g - \dfrac{1}{2}\log (L) = k'' \cdot log (L),$$
o que não representa uma função do primeiro grau. Portanto
$$\boxed{\text{Letra} \ E}$$

