A figura mostra uma barra homogênea de massa em equilíbrio. Ela está sustentada por um fio em uma de suas extremidades e é impedida de cair devido ao atrito com a parede na outra extremidade. A aceleração da gravidade vale .
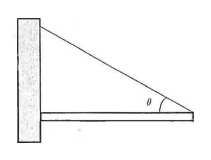
A força total exercida pela parede sobre a barra vale:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

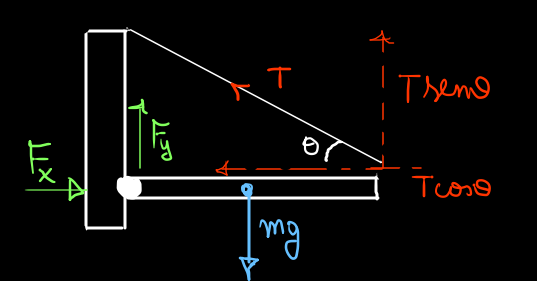
Seja $T$ a tração da corda , $N$ a força normal que a parede exerce sobre a barra , $fat$ o atrito atuante sobre a barra , $2x$ o comprimento da barra e $F$ a força desejada.
Analisaremos primeiramente esse sistema em relação ao momento de força(torque) , considere a extremidade da barra que está em contato com a parede como sendo o pólo adotado.Como a barra está em equilíbrio e é homogênea podemos dizer que o torque do peso da barra é igual a $mg \cdot x$ que é igual ao torque gerado pela componente vertical $T\sin\theta$ da tração , sendo este torque igual a $T\sin\theta \cdot 2x$
$\therefore$
$T\sin\theta \cdot 2x = mg \cdot x \implies 2T\sin\theta = mg \implies \boxed{T = \dfrac{mg}{2\sin\theta}}$
Agora iremos analisar o equilíbrio de translação , analisando as forças atuantes na horizontal podemos afirmar que
$N = T\cos\theta = \boxed{N= \dfrac{mg\cdot \cos\theta}{2\sin\theta}}$
analisando as forças atuantes na vertical podemos encontrar que
$fat + T\sin\theta = mg = fat + \dfrac{mg}{2} = mg \implies \boxed{fat = \dfrac{mg}{2}}$
Note que a força $F$ é dado por $F = \sqrt{fat^2 + N^2}$
$\therefore$
$F = \sqrt{\left(\dfrac{mg}{2}\right)^2 +\left(\dfrac{mg \cdot \cos\theta}{2\sin\theta}\right)^2 } = \sqrt{\left(\dfrac{mg}{2}\right)^2\cdot \left(1 + \dfrac{\cos^2\theta}{\sin^2\theta} \right)}$
$= F = \sqrt{\left(\dfrac{mg}{2}\right)^2\cdot \left( \dfrac{1}{\sin^2\theta} \right)} = F = \dfrac{mg}{2} \cdot \dfrac{1}{\sin\theta}$
$= \boxed{F = \dfrac{mg}{2\sin\theta}} $
Ampliar Imagem


