USP 2017 Matemática - Questões

Um analgésico é aplicado via intravenosa. Sua concentração no sangue, até atingir a concentração nula, varia com o tempo de acordo com a seguinte relação:

$$c(t) = 400 - k\cdot \log_3\ (a\cdot t + 1),$$

em que $t$ é dado em horas e $c(t)$ é dado em $\text{mg/L}$. As constantes $a$ e $k$ são positivas.

a) Qual é a concentração do analgésico no instante inicial $t = 0$?

b) Calcule as constantes $a$ e $k$, sabendo que, no instante $t = 2$, a concentração do analgésico no sangue é metade da concentração no instante inicial e que, no instante $t = 8$, a concentração do analgésico no sangue é nula.

Sejam $a$ e $b$ dois números inteiros positivos. Diz-se que $a$ e $b$ são equivalentes se a soma dos divisores positivos de $a$ coincide com a soma dos divisores positivos de $b$. Constituem dois inteiros positivos equivalentes:

O paralelepípedo reto-retângulo $ABCDEFGH$ representado na figura, tem medida dos lados $\overline{AB} = 4$, $\overline{BC}=2$ e $\overline{BF}=2$.

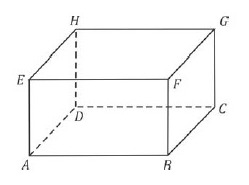
O seno do ângulo $H\widehat{A}F$ é igual a

João tem R$ $150,00$ para comprar canetas em $3$ lojas. Na loja $A$, as canetas são vendidas em dúzias, cada dúzia custa R$ $40,00$ e há apenas $2$ dúzias em estoque. Na loja $B$, as canetas são vendidas em pares, cada par custa R$ $7,60$ e há $10$ pares em estoque. Na loja $C$, as canetas são vendidas avulsas, cada caneta custa R$ $3,20$ e há $25$ canetas em estoque. O maior número de canetas que João pode comprar nas lojas $A, B$ e $C$ utilizando no máximo R$ $150,00$ é igual a

Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo-secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é