USP 2014 - Questões

Leia o seguinte extrato de uma reportagem do jornal inglês The Guardian, de 22 de janeiro de 2013, para em seguida atender ao que se pede:

O ministro de finanças do Japão, Taro Aso, disse na segunda-feira (dia 21) que os velhos deveriam "apressar-se a morrer", para aliviar a pressão que suas despesas médicas exercem sobre o Estado.

"Deus nos livre de uma situação em que você é forçado a viver quando você quer morrer. Eu acordaria me sentindo cada vez pior se soubesse que o tratamento é todo pago pelo governo", disse ele durante uma reunião do conselho nacional a respeito das reformas na seguridade social. "O problema não será resolvido, a menos que você permita que eles se apressem a morrer".

Os comentários de Aso são suscetíveis de causar ofensa no Japão, onde quase um quarto da população de 128 milhões tem mais de 60 anos. A proporção deve atingir 40% nos próximos 50 anos.

Aso, de 72 anos de idade, que tem funções de vice-primeiro-ministro, disse que iria recusar os cuidados de fim de vida. "Eu não preciso desse tipo de atendimento", declarou ele em comentários citados pela imprensa local, acrescentando que havia redigido uma nota instruindo sua família a negar-lhe tratamento médico para prolongar a vida.

Para maior agravo, ele chamou de "pessoas-tubo" os pacientes idosos que já não conseguem se alimentar sozinhos. O ministério da saúde e do bem-estar, acrescentou, está "bem consciente de que custa várias dezenas de milhões de ienes" por mês o tratamento de um único doente em fase final de vida.

Mais tarde, Aso tentou explicar seus comentários. Ele reconheceu que sua linguagem fora "inapropriada" em um fórum público e insistiu que expressara apenas sua preferência pessoal. "Eu disse o que eu, pessoalmente, penso, não o que o sistema de assistência médica a idosos deve ser", declarou ele a jornalistas.

Não foi a primeira vez que Aso, um dos mais ricos políticos do Japão, questionou o dever do Estado para com sua grande população idosa. Anteriormente, em um encontro de economistas, ele já dissera: "Por que eu deveria pagar por pessoas que apenas comem e bebem e não fazem nenhum esforço? Eu faço caminhadas todos os dias, além de muitas outras coisas, e estou pagando mais impostos".

(theguardian.com, Tuesday, 22 January 2013. Traduzido e adaptado.)

Considere as opiniões atribuídas ao referido político japonês, tendo em conta que elas possuem implicações éticas, culturais, sociais e econômicas capazes de suscitar questões de várias ordens: essas opiniões são tão raras ou isoladas quanto podem parecer? O que as motiva? O que elas dizem sobre as sociedades contemporâneas? Opiniões desse teor seriam possíveis no contexto brasileiro? Como as jovens gerações encaram os idosos?

Escolhendo, entre os diversos aspectos do tema, os que você considerar mais relevantes, redija uma redação dissertativa-argumentativa, no qual você avalie as posições do citado ministro, supondo que esse texto se destine à publicação - seja em um jornal, uma revista ou em um site da internet.

Uma circunferência de raio $3\ \text{cm}$ está inscrita no triângulo isósceles $ABC$, no qual $\overline{AB}=\ \overline{AC}$. A altura relativa ao lado $\overline{BC}$ mede $8\ \text{cm}$. O comprimento de $\overline{BC}$ é, portanto, igual a

Uma das piscinas do Centro de Práticas Esportivas da $USP$ tem o formato de três hexágonos regulares congruentes, justapostos, de modo que cada par de hexágonos tem um lado em comum, conforme representado na figura abaixo. A distância entre lados paralelos de cada hexágono é de $25$ metros.

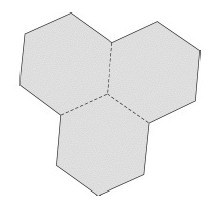
Assinale a alternativa que mais se aproxima da área da piscina.

O triângulo $AOB$ é isósceles, com $OA=OB$, e $ABCD$ é um quadrado. Sendo $\theta$ a medida do ângulo $A\text{Ô}B$, pode-se garantir que a área do quadrado é maior do que a área do triângulo se:

Dados os valores aproximados:

${\hspace{2pt}\mathrm{tg}\ (14^\circ) \cong 0,2493}$

${\hspace{2pt}\mathrm{tg}\ (15^\circ) \ }\cong 0,2679$

${\hspace{2pt}\mathrm{tg}\ (20^\circ) \ }\cong 0,3640$

${\hspace{2pt}\mathrm{tg}\ (28^\circ) \ }\cong 0,5317$

Considere o triângulo $ABC$ no plano cartesiano com vértices $A=\ (0,0)$, $B=\ (3,4)$ e $C=\ (8,0)$. O retângulo $MNPQ$ tem os vértices $M$ e $N$ sobre o eixo das abscissas, o vértice $Q$ sobre o lado $\overline{AB}$ e o vértice $P$ sobre o lado $\overline{BC}$. Dentre todos os retângulos construídos desse modo, o que tem área máxima é aquele em que o ponto $P$ é