USP 2012 Física - Questões

Nina e José estão sentados em cadeiras, diametralmente opostas, de uma roda gigante que gira com velocidade angular constante. Num certo momento, Nina se encontra no ponto mais alto do percurso e José, no mais baixo; após $15\ \text{s}$, antes de a roda completar uma volta, suas posições estão invertidas. A roda gigante tem raio $R = 20\ \text{m}$ e as massas de Nina e José são, respectivamente, $M_N=60\ \text{kg}$ e $M_J = 70\ \text{kg}$. Calcule

NOTE E ADOTE

$\pi =3$

Aceleração da gravidade $g=10\ \text{m/s}^2$

1. a) O módulo $v$ da velocidade linear das cadeiras da roda gigante;
   

2. b) O módulo $a_R$ da aceleração radial de Nina e de José;
   

3. c) Os módulos $N_N$ e $N_J$ das forças normais que as cadeiras exercem, respectivamente, sobre Nina e sobre José no instante em que Nina se encontra no ponto mais alto do percurso e José, no mais baixo.
   

Em um laboratório de física, estudantes fazem um experimento em que radiação eletromagnética de comprimento de onda ${\lambda } = 300\ nm$ incide em uma placa de sódio, provocando a emissão de elétrons. Os elétrons escapam da placa de sódio com energia cinética máxima $E_C=E-W$, sendo $E$ a energia de um fóton da radiação e $W$ a energia mínima necessária para extrair um elétron da placa. A energia de cada fóton é $E = h\cdot f$, sendo $h$ a constante de Planck e $f$ a frequência da radiação. Determine

NOTE E ADOTE

Velocidade da radiação eletromagnética: $c = 3\ \times \ {10}^8\ m/s.$

$1\ nm = {10}^{-9}\ m.$

$h = 4\ \times \ {10}^{-15}\ eV.s.$

$W\ (\text{sódio}) = 2,3\ eV.$

$1\ eV = 1,6\ \times \ {10}^{-19}\ J.$

1. a) A frequência $f$ da radiação incidente na placa de sódio;
   

2. b) A energia $E$ de um fóton dessa radiação;
   

3. c) A energia cinética máxima $E_C$ de um elétron que escapa da placa de sódio;
   

4. d) A frequência $f_0$ da radiação eletromagnética, abaixo da qual é impossível haver emissão de elétrons da placa de sódio.
   

Uma pequena bola de borracha maciça é solta do repouso de uma altura de $1\ \text{m}$ em relação a um piso liso e sólido. A colisão da bola com o piso tem coeficiente de restituição $\varepsilon = 0,8$. A altura máxima atingida pela bola, depois da sua terceira colisão com o piso, é

NOTE E ADOTE

Suponha que $\varepsilon =v^2_f/v^2_i$, em que $v_f$ e $v_i$ são, respectivamente, os módulos das velocidades da bola logo após e imediatamente antes da colisão com o piso.

Aceleração da gravidade $g=10\ \text{m/s}^2$

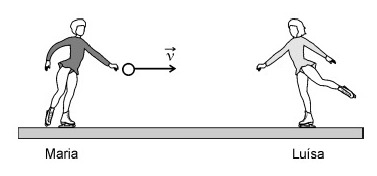
Maria e Luísa, ambas de massa $M$, patinam no gelo. Luísa vai ao encontro de Maria com velocidade de módulo $V$. Maria, parada na pista, segura uma bola de massa $m$ e, num certo instante, joga a bola para Luísa. A bola tem velocidade de módulo ${v}$, na mesma direção de $\overrightarrow{V}$. Depois que Luísa agarra a bola, as velocidades de Maria e Luísa, em relação ao solo, são, respectivamente,

NOTE E ADOTE

$V$ e $v$ são velocidades em relação ao solo.

Considere positivas as velocidades para a direita.

Desconsidere efeitos dissipativos.

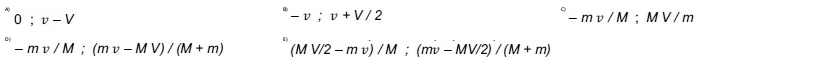
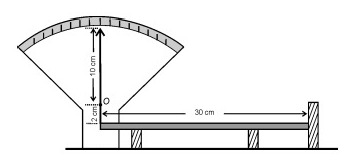
Para ilustrar a dilatação dos corpos, um grupo de estudantes apresenta, em uma feira de ciências, o instrumento esquematizado na figura acima. Nessa montagem, uma barra de alumínio com $30\ \text{cm}$ de comprimento está apoiada sobre dois suportes, tendo uma extremidade presa ao ponto inferior do ponteiro indicador e a outra encostada num anteparo fixo. O ponteiro pode girar livremente em torno do ponto $\textit{O}$, sendo que o comprimento de sua parte superior é

$10\ \text{cm}$ e, o da inferior, $2\ \text{cm}$. Se a barra de alumínio, inicialmente à temperatura de $25\ ^\circ C$, for aquecida a $225\ ^\circ C$, o deslocamento da extremidade superior do ponteiro será, aproximadamente, de

NOTE E ADOTE

Coeficiente de dilatação linear do alumínio: $2\ \times \ {10}^{-5}\ {^\circ C}^{-1}$.