USP 2012 - Questões

O segmento $\overline{AB}$ é lado de um hexágono regular de área $\sqrt{3}$. O ponto $P$ pertence à mediatriz de $\overline{AB}$ de tal modo que a área do triângulo $PAB$ vale $\sqrt{2}$. Então, a distância de $P$ ao segmento $\overline{AB}$ é igual a

Considere a função

$$f\left(x\right)=1-\dfrac{4x}{{\left(x+1\right)}^2}\ ,$$

a qual está definida para $x\neq -1$. Então, para todo $x\neq 1$ e $x\neq -1$, o produto $f\left(x\right)f(-x)$ é igual a

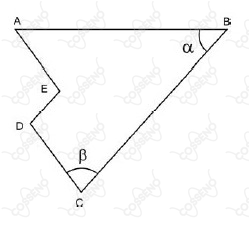
Na figura, tem-se $\overline{AE}$ paralelo a $\overline{CD}$, $\overline{BC}$ paralelo a $\overline{DE}$, $AE=2$, $\alpha =45\ ^\circ$ e $\beta =75^\circ$. Nessas condições, a distância do ponto $E$ ao segmento $\overline{AB}$ é igual a:

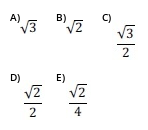
No plano cartesiano $Oxy$, a circunferência $C$ é tangente ao eixo $Ox$ no ponto de abscissa $5$ e contém o ponto $(1,\ 2)$. Nessas condições, o raio de C vale

Em um tetraedro regular de lado $a$, a distância entre os pontos médios de duas arestas não adjacentes é igual a