UNICAMP 2019 Física - Questões

Nos cruzamentos de avenidas das grandes cidades é comum encontrarmos, além dos semáforos tradicionais de controle de tráfego de carros, semáforos de fluxo de pedestres, com cronômetros digitais que marcam o tempo para a travessia na faixa de pedestres.

1. a) No instante em que o semáforo de pedestres se torna verde e o cronômetro inicia a contagem regressiva, uma pessoa encontra-se a uma distância $d = 20\ \text{m}$ do ponto de início da faixa de pedestres, caminhando a uma velocidade inicial $v_0 = 0,5\ \text{m/s}$. Sabendo que ela inicia a travessia da avenida com velocidade $v = 1,5\ \text{m/s}$, calcule a sua aceleração constante no seu deslocamento em linha reta até o início da faixa.
   

2. b) Considere agora uma pessoa que atravessa a avenida na faixa de pedestres, partindo de um lado da avenida com velocidade inicial $v_0 = 0,4\ \text{m/s}$ e chegando ao outro lado com velocidade final $v = 1,2\ \text{m/s}$. O pedestre realiza todo o percurso com aceleração constante em um intervalo de tempo de $t = 15\ \text{s}$. Construa o gráfico da velocidade do pedestre em função do tempo e, a partir do gráfico, calcule a largura da avenida.
   

O físico inglês Stephen Hawking $(1942-2018)$, além de suas contribuições importantes para a cosmologia, a física teórica e sobre a origem do universo, nos últimos anos de sua vida passou a sugerir estratégias para salvar a raça humana de uma possível extinção, entre elas, a mudança para outro planeta. Em abril de $2018$, uma empresa americana, em colaboração com a Nasa, lançou o satélite $TESS$, que analisará cerca de vinte mil planetas fora do sistema solar. Esses planetas orbitam estrelas situadas a menos de trezentos $anos-luz$ da Terra, sendo que um ano-luz é a distância que a luz percorre no vácuo em um ano. Considere um ônibus espacial atual que viaja a uma velocidade média $v=2,0\times 10^4\ \text{km/s}$. O tempo que esse ônibus levaria para chegar a um planeta a uma distância de $100\ anos-luz$ é igual a

Dado: A velocidade da luz no vácuo é igual a $c = 3,0 \times 10^8\ m/s$

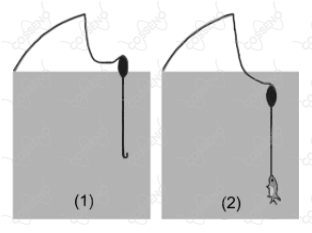
Em uma pescaria é utilizada uma linha com boia e anzol. Inicialmente, na posição de espera, a linha acima da boia mantém-se frouxa e a boia flutua, ficando com $1/3$ do seu volume submerso $($ figura $1)$. Quando o peixe é fisgado, a boia é puxada, ficando totalmente submersa e momentaneamente parada; simultaneamente, a linha que a une ao anzol fica esticada verticalmente $($ figura $2)$. A parte superior da linha, acima da boia, mantém-se frouxa. Nessa situação, quanto vale o módulo da tensão da linha que une a boia ao anzol? Despreze as massas da linha e do anzol, bem como o atrito viscoso com a água.

Drones vêm sendo utilizados por empresas americanas para monitorar o ambiente subaquático. Esses drones podem substituir mergulhadores, sendo capazes de realizar mergulhos de até cinquenta metros de profundidade e operar por até duas horas e meia.

Considere um drone que utiliza uma bateria com carga total $Q=900\ \text{mAh}$. Se o drone operar por um intervalo de tempo igual a $\Delta t=90\ \text{min}$, a corrente média fornecida pela bateria nesse intervalo de tempo será igual a

Drones vêm sendo utilizados por empresas americanas para monitorar o ambiente subaquático. Esses drones podem substituir mergulhadores, sendo capazes de realizar mergulhos de até cinquenta metros de profundidade e operar por até duas horas e meia.

Frequentemente esses drones são usados para medir a temperatura da água $T$ em função da profundidade $d$, a partir da superfície ($d=0$), como no caso ilustrado no gráfico a seguir (dados adaptados).

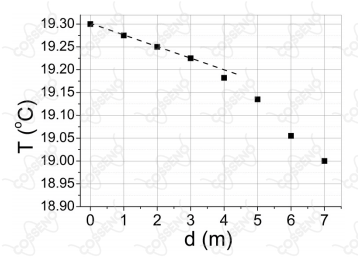
Considere que a densidade da água é $\rho=1000\ \text{kg/m}^3$ e constante para todas as profundidades medidas pelo drone. Qual é a diferença de pressão hidrostática entre a superfície e uma profundidade para a qual a temperatura da água é $T=19\ ^\circ \text{C}$?