UNB 2010 - Questões

No sistema de coordenadas cartesianas xOy, cuja unidade de medida de comprimento é o centímetro, o ponto (x, y) é identificado com o número complexo z = x + yi, em que x = Re(z) é a parte real, y = Im(z) é a parte imaginária e i é a unidade imaginária. Nesse sistema, considere que, em certo instante, uma partícula ocupa a posição P = (x, y) e que Q = (x', y') seja um ponto do plano, com $P\ne Q$. Considere as matrizes $A=\left[\begin{matrix}cos\theta&-sen\theta\\sen\theta&cos\theta\end{matrix}\right],$ $B=\left[\begin{matrix}3&0\\0&2\end{matrix}\right]$ e $C=A-\lambda I_2$, em que I₂ denota a matriz identidade de ordem 2, e $\lambda$ e $\theta$ são números reais com $0<\theta\le2\pi$.

Representando os pontos P e Q pelas matrizes colunas $P=\left[\begin{matrix}x\\y\end{matrix}\right]$ e e tendo por base as informações acima, julgue o item.

Para algum valor de θ, 0 < θ ≤ 2π, a equação det C = 0 possui duas raízes reais distintas.

A figura acima apresenta algumas informações a respeito de Marte, planeta que mais se assemelha à Terra no sistema solar. Dados recentes obtidos pela NASA confirmam a existência de água na forma de gelo nesse planeta. Considerando, além dessas informações, que a pressão atmosférica na superfície de Marte seja de 0,006 atm, que as órbitas da Terra e de Marte sejam circulares, que a constante de gravitação universal seja igual a 6,67 × 10^-11 N•m²•kg^-2 e que a aceleração gravitacional na Terra seja igual a 10 m/s², julgue o item.

Se a massa óssea de um astronauta sofresse decréscimo de 2% a cada mês de viagem no espaço devido à falta de peso, então, tomando-se 0,3010 e -0,0088 como valores aproximados, respectivamente, de log 2 e log 0,98, é correto afirmar que, se um astronauta iniciar uma viagem a Marte em março de 2015, sua massa óssea estará reduzida à metade antes de 2018.

Pode-se determinar o instante da morte de um organismo utilizando-se a Lei de Resfriamento de Newton, segundo a qual a taxa de variação da temperatura de um corpo é proporcional à diferença entre as temperaturas do corpo e do meio externo. Nesse sentido, suponha que, na investigação de um homicídio, a temperatura do cadáver encontrado, em ºC, t horas (h) após o óbito, seja dada pela função T =T(t) = 22 + 10 e^-k1 , em que: t₀ = 0 representa o instante em que o corpo foi encontrado; t < 0 corresponde, em módulo, à quantidade de horas decorridas antes da descoberta do cadáver; t > 0 representa a quantidade de horas decorridas desde a descoberta do corpo; e k é uma constante positiva.

Admitindo que, nessa situação hipotética, na hora do óbito, a temperatura do corpo era de 37 ^oC e que, duas horas após a descoberta do corpo, a temperatura era de 25 ºC e considerando ln 2 = 0,7, ln 3 = 1,1, ln 5 = 1,6, julgue:

A função T = T(t) é inversível e sua inversa é dada por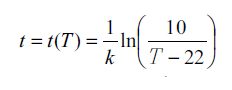 

Pode-se determinar o instante da morte de um organismo utilizando-se a Lei de Resfriamento de Newton, segundo a qual a taxa de variação da temperatura de um corpo é proporcional à diferença entre as temperaturas do corpo e do meio externo. Nesse sentido, suponha que, na investigação de um homicídio, a temperatura do cadáver encontrado, em ºC, t horas (h) após o óbito, seja dada pela função T =T(t) = 22 + 10 e^-k1 , em que: t₀ = 0 representa o instante em que o corpo foi encontrado; t < 0 corresponde, em módulo, à quantidade de horas decorridas antes da descoberta do cadáver; t > 0 representa a quantidade de horas decorridas desde a descoberta do corpo; e k é uma constante positiva.

Admitindo que, nessa situação hipotética, na hora do óbito, a temperatura do corpo era de 37 ^oC e que, duas horas após a descoberta do corpo, a temperatura era de 25 ºC e considerando ln 2 = 0,7, ln 3 = 1,1, ln 5 = 1,6, julgue:

Com base nos dados, conclui-se que o óbito ocorreu 40 minutos antes da descoberta do cadáver.

Pode-se determinar o instante da morte de um organismo utilizando-se a Lei de Resfriamento de Newton, segundo a qual a taxa de variação da temperatura de um corpo é proporcional à diferença entre as temperaturas do corpo e do meio externo. Nesse sentido, suponha que, na investigação de um homicídio, a temperatura do cadáver encontrado, em ºC, t horas (h) após o óbito, seja dada pela função T =T(t) = 22 + 10 e^-k1 , em que: t₀ = 0 representa o instante em que o corpo foi encontrado; t < 0 corresponde, em módulo, à quantidade de horas decorridas antes da descoberta do cadáver; t > 0 representa a quantidade de horas decorridas desde a descoberta do corpo; e k é uma constante positiva.

Admitindo que, nessa situação hipotética, na hora do óbito, a temperatura do corpo era de 37 ^oC e que, duas horas após a descoberta do corpo, a temperatura era de 25 ºC e considerando ln 2 = 0,7, ln 3 = 1,1, ln 5 = 1,6, julgue:

À medida que t aumenta, T = T(t) tende a se aproximar da temperatura de 22 ºC, mas nunca chega a atingi-la.