UERJ 2020 Matemática - Questões

Juros e taxas de financiamentos imobiliários explodem dívida real

Os financiamentos imobiliários surpreendem os clientes. Ao longo do tempo, os juros e as taxas de correção monetária de seus empréstimos fazem com que os valores de suas dívidas reais sejam bem mais altos do que o esperado. Esse aumento é expresso pela metáfora contida no verbo “explodir”.

Considere que, após o pagamento de $24$ parcelas mensais de R$ 1.000,00 mais os juros e taxas estabelecidos pelo banco, um cliente esperava que sua dívida real fosse reduzida em R$ 24.000,00.

Porém, a redução foi de R$ 16.000,00.

Em relação a R$ 24.000,00, o valor de R$ 16.000,00 representa um percentual que está mais próximo de:

Admita que, para escovar os dentes, seja necessário, em média, $1$ litro de água. Caso a torneira permaneça aberta durante toda a escovação, serão gastos, em média, $11$ litros, havendo desperdício de $10$ litros.

Considere uma família de quatro pessoas que escovam os dentes três vezes ao dia, mantendo a torneira aberta.

Em $365$ dias, o desperdício de água dessa família, em litros, será igual a:

Os números inteiros $x$ e $y$ satisfazem às seguintes equações:

$$\begin{cases} \dfrac{2}{5}\cdot x+ \dfrac{3}{5}\cdot y=37\\ \\ x-y=30 \end{cases}$$

Logo, $x + y$ é igual a:

A imagem a seguir representa um cubo com aresta de $2$ cm. Nele, destaca-se o triângulo $AFC$.

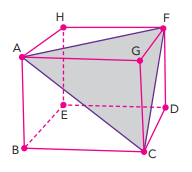
A projeção ortogonal do triângulo $AFC$ no plano da base $BCDE$ do cubo é um triângulo de área $y$.

O valor de $y$, em $\text{cm}^2$ , é igual a:

Ao se aposentar aos $65$ anos, um trabalhador recebeu seu Fundo de Garantia por Tempo de Serviço ($FGTS$) no valor de R$ $50.000,00$ e resolveu deixá-lo em uma aplicação bancária, rendendo juros compostos de 4% ao ano, até obter um saldo de R$ $100.000,00$. Se esse rendimento de 4% ao ano não mudar ao longo de todos os anos, o trabalhador atingirá seu objetivo após $x$ anos. Considerando $\text{log} \ (1,04) = 0,017 \ \text{e} \ \text{log} \ 2 = 0,301$, o valor mais próximo de $x$ é: