UERJ 2016 Matemática - Questões

Com o objetivo de melhorar o tráfego de veículos, a prefeitura de uma grande cidade propôs a construção de quatro terminais de ônibus. Para estabelecer conexão entre os terminais, foram estipuladas as seguintes quantidades de linhas de ônibus:

• do terminal A para o B, 4 linhas distintas;

• do terminal B para o C, 3 linhas distintas;

• do terminal A para o D, 5 linhas distintas;

• do terminal D para o C, 2 linhas distintas.

Não há linhas diretas entre os terminais A e C.

Supondo que um passageiro utilize exatamente duas linhas de ônibus para ir do terminal A para o terminal C, calcule a quantidade possível de trajetos distintos que ele poderá fazer.

Admita a seguinte sequência numérica para o número natural $n$:

$$a_{1} =\dfrac{1}{3} \text{ e } a_{n} =a_{n-1} +3$$

Sendo $2\le n\le 10$, os dez elementos dessa sequência, em que $a_{1} =\dfrac{1}{3}$ e $a_{10} =\dfrac{82}{3}$, são:

$$\left(\dfrac{1}{3} ,\ \dfrac{10}{3} ,\ \dfrac{19}{3} ,\ \dfrac{28}{3} ,\ \dfrac{37}{3} ,\ a_{6} ,\ a_{7} ,\ a_{8} ,\ a_{9} ,\ \dfrac{82}{3} \right)$$ A média aritmética dos quatro últimos elementos da sequência é igual a:

Observe a função $f$, definida por: $$f\left(x\right)=x^2-2kx+29,\ \ \ \ \ \text{para }x\in \mathbb{R}$$ Se $f\left(x\right)\ge 4$, para todo número real $x$, o valor mínimo da função $f$ é $4$.

Assim, o valor positivo do parâmetro $k$ é:

Dois dados, com doze faces pentagonais cada um, têm a forma de dodecaedros regulares. Se os dodecaedros estão justapostos por uma de suas faces, que coincidem perfeitamente, formam um poliedro côncavo, conforme ilustra a figura.

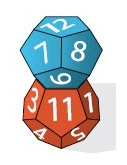
Considere o número de vértices $V$, de faces $F$ e de arestas $A$ desse poliedro côncavo.

A soma $V+F+A$ é igual a:

Admita que a ordem de grandeza de uma medida $x$ é uma potência de base $10$, com expoente

$n$ inteiro, para ${10}^{n-\frac{1}{2}}\le x<{10}^{n+\frac{1}{2}}$.

Considere que um terremoto tenha liberado uma energia $E$, em joules, cujo valor numérico é tal que $\log_{10}\ E =15,3$.

A ordem de grandeza de $E$, em joules, equivale a: