UEL 2019 Matemática - Questões
Abrir Opções Avançadas
Uma estratégia para obter efeito humorístico em quadrinhos é atribuir a objetos abstratos características e ações tipicamente humanas. A figura a seguir é um exemplo de aplicação desse recurso.
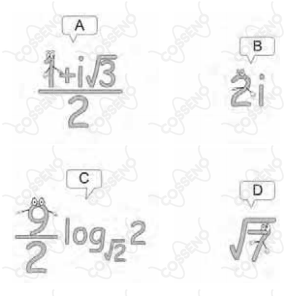
Supondo que cada número diga uma verdade matemática sobre si mesmo, relacione as frases (de I a IV) aos balões de diálogo (de A a D).
I) Meu cubo é irracional.
II) Sou racional.
III) Sou puramente imaginário.
IV) Meu inverso multiplicativo coincide com meu conjugado.

Assinale a alternativa que contém a associação correta.
Convenciona-se que o tamanho dos televisores, de tela plana e retangular, é medido pelo comprimento da diagonal da tela, expresso em polegadas. Define-se a proporção dessa tela como sendo o quociente do lado menor pelo lado maior, também em polegadas. Essas informações estão dispostas na figura a seguir.
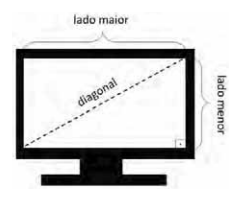
Suponha que Eurico e Hermengarda tenham televisores como dado na figura e de proporção $\dfrac{3}{4}$. Sabendo que o tamanho do televisor de Hermengarda é 5 polegadas maior que o de Eurico, assinale a alternativa que apresenta, corretamente, quantas polegadas o lado maior da tela do televisor de Hermengarda excede o lado correspondente do televisor de Eurico.
Conforme um fármaco é injetado, a partir do instante $t = 0$, sua concentração no sangue aumenta até atingir um máximo $C$ em $t = T_m$. Considere que, na sequência, o rim inicie o processo de excreção do fármaco, fazendo com que sua concentração no sangue caia progressivamente. Suponha que a função $f : \mathbb{R}^+ \to \mathbb{R}$ determine a concentração $f(t)$ desse fármaco no sangue em um instante de tempo $t \geq 0$. Sabendo que $f(t)=C\left(\dfrac{t}{T_m} \right)^2$ se $t < T_m$, e considerando que $f(t) = C2^{T_m}2^{-t}$ se $t \geq T_m$, com $T_m$ e $C$ constantes positivas, assinale a alternativa que apresenta, corretamente, os dois instantes de tempo em que a concentração desse fármaco no sangue é $\dfrac{C}{2}$
O filme Jumanji (1995) é uma obra de ficção que retrata a história de um jogo de tabuleiro mágico que empresta seu nome ao longa-metragem. O jogo é composto de dois dados distinguíveis de 6 lados, um tabuleiro com um visor de cristal no centro e peças que representam cada jogador. No filme, Alan Parrish é um garoto que encontra o jogo em um local de construção e o leva para casa. Assim que chega, Alan convida Sarah Whittle, uma garota da vizinhança, para jogar. Quando Alan lança os dados, aparece no visor a seguinte mensagem:

Adaptado de google.com.br
Alan então é sugado pelo visor de cristal e transportado magicamente até a selva de Jumanji. Supondo que os dois dados do jogo sejam independentes e honestos, assinale a alternativa que apresenta, corretamente, a probabilidade de algum jogador lançar os dois dados e obter a soma de 5 ou 8, de modo a tirar Alan da selva.
Leia o texto a seguir.
Foi ali no meio da praça. [...] Zuzé Paraza, pintor reformado, tossiu sacudindo a magreza do seu todo corpo. Então, assim contam os que viram, ele vomitou um corvo vivo. O pássaro saiu inteiro das entranhas dele. [...] Estivera tanto tempo lá dentro que já sabia falar.
COUTO, Mia. O último aviso do corvo falador. In: Vozes anoitecidas. São Paulo: Companhia das Letras, 2015. p. 29.
Zuzé desafiou o corvo falador. De dentro de seu gabinete, Zuzé mostrou ao corvo a seguinte tabela.
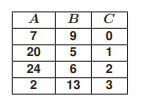
Zuzé solicita ao corvo que pense em uma equação matemática que relacione, linha a linha, os números das colunas $A$, $B$ e $C$ da tabela. Prontamente o corvo falante responde: $i^{A+B} = i^C$, onde $i$ é a unidade imaginária.
Com base na equação dita pelo corvo e sabendo que $A,\ B$ e $C$ são números naturais, considere as afirmativas a seguir.
I) Se $A + B$ é múltiplo de 4 e $C = 4$, então $A, \ B$ e $C$ satisfazem a equação.
II) Se $A = 26, \ B = 44$ e $C = 30$, então $A, \ B$ e $C$ satisfazem a equação.
III) Se $A = B = 1$, então a única possibilidade para que $A, \ B$ e $C$ satisfaçam a equação é $C = 6$.
IV) Se $A$ e $B$ são números ímpares e $C = 1$, então $A, \ B$ e $C$ satisfazem a equação.
Assinale a alternativa correta.
Carregando...