UEL 2019 - Questões

Conforme um fármaco é injetado, a partir do instante $t = 0$, sua concentração no sangue aumenta até atingir um máximo $C$ em $t = T_m$. Considere que, na sequência, o rim inicie o processo de excreção do fármaco, fazendo com que sua concentração no sangue caia progressivamente. Suponha que a função $f : \mathbb{R}^+ \to \mathbb{R}$ determine a concentração $f(t)$ desse fármaco no sangue em um instante de tempo $t \geq 0$. Sabendo que $f(t)=C\left(\dfrac{t}{T_m} \right)^2$ se $t < T_m$, e considerando que $f(t) = C2^{T_m}2^{-t}$ se $t \geq T_m$, com $T_m$ e $C$ constantes positivas, assinale a alternativa que apresenta, corretamente, os dois instantes de tempo em que a concentração desse fármaco no sangue é $\dfrac{C}{2}$

Leia o texto a seguir.

No Brasil, o sistema de voto proporcional funciona assim: aplicam-se os chamados quocientes eleitoral e partidário. O quociente eleitoral é definido pela soma do número de votos válidos (V) – que são os votos de legenda e os votos nominais, excluindo-se os brancos e os nulos – dividida pelo número de cadeiras em disputa (C).

A partir daí, calcula-se o quociente partidário, que é o resultado do número de votos válidos obtidos pelo partido isolado ou pela coligação, dividido pelo quociente eleitoral. O quociente partidário é um número fundamental, pois ele indica quantas cadeiras poderão ser ocupadas pelos candidatos aptos do respectivo partido ou coligação.

Adaptado de Revista Eletrônica da Escola Judiciária Eleitoral. Número 5. Ano 3.

Considere que a eleição para vereador em Amado Florêncio funciona como descrito anteriormente. Suponha que existam 12 cadeiras em disputa e que nesta eleição para vereador a soma do número dos votos válidos seja de 3996. A coligação “Por uma Nova Amado Florêncio” obteve 333 votos válidos. Já a coligação “Amado Florêncio Renovada” obteve 666 votos válidos.

Assinale a alternativa que apresenta, correta e respectivamente, o quociente partidário dessas coligações: “Por uma Nova Florêncio” e “Amado Florêncio Renovada”.

Uma estratégia para obter efeito humorístico em quadrinhos é atribuir a objetos abstratos características e ações tipicamente humanas. A figura a seguir é um exemplo de aplicação desse recurso.

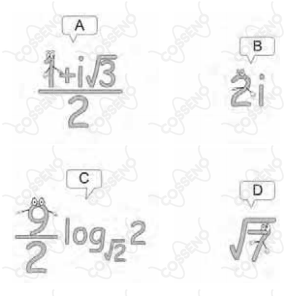
Supondo que cada número diga uma verdade matemática sobre si mesmo, relacione as frases (de I a IV) aos balões de diálogo (de A a D).

1. I) Meu cubo é irracional.
   

2. II) Sou racional.
   

3. III) Sou puramente imaginário.
   

4. IV) Meu inverso multiplicativo coincide com meu conjugado.
   

Assinale a alternativa que contém a associação correta.

O filme Jumanji (1995) é uma obra de ficção que retrata a história de um jogo de tabuleiro mágico que empresta seu nome ao longa-metragem. O jogo é composto de dois dados distinguíveis de 6 lados, um tabuleiro com um visor de cristal no centro e peças que representam cada jogador. No filme, Alan Parrish é um garoto que encontra o jogo em um local de construção e o leva para casa. Assim que chega, Alan convida Sarah Whittle, uma garota da vizinhança, para jogar. Quando Alan lança os dados, aparece no visor a seguinte mensagem:

Adaptado de google.com.br

Alan então é sugado pelo visor de cristal e transportado magicamente até a selva de Jumanji. Supondo que os dois dados do jogo sejam independentes e honestos, assinale a alternativa que apresenta, corretamente, a probabilidade de algum jogador lançar os dois dados e obter a soma de 5 ou 8, de modo a tirar Alan da selva.

Leia o texto a seguir.

Foi ali no meio da praça. [...] Zuzé Paraza, pintor reformado, tossiu sacudindo a magreza do seu todo corpo. Então, assim contam os que viram, ele vomitou um corvo vivo. O pássaro saiu inteiro das entranhas dele. [...] Estivera tanto tempo lá dentro que já sabia falar.

COUTO, Mia. O último aviso do corvo falador. In: Vozes anoitecidas. São Paulo: Companhia das Letras, 2015. p. 29.

Zuzé desafiou o corvo falador. De dentro de seu gabinete, Zuzé mostrou ao corvo a seguinte tabela.

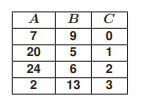
Zuzé solicita ao corvo que pense em uma equação matemática que relacione, linha a linha, os números das colunas $A$, $B$ e $C$ da tabela. Prontamente o corvo falante responde: $i^{A+B} = i^C$, onde $i$ é a unidade imaginária.

Com base na equação dita pelo corvo e sabendo que $A,\ B$ e $C$ são números naturais, considere as afirmativas a seguir.

1. I) Se $A + B$ é múltiplo de 4 e $C = 4$, então $A, \ B$ e $C$ satisfazem a equação.
   

2. II) Se $A = 26, \ B = 44$ e $C = 30$, então $A, \ B$ e $C$ satisfazem a equação.
   

3. III) Se $A = B = 1$, então a única possibilidade para que $A, \ B$ e $C$ satisfaçam a equação é $C = 6$.
   

4. IV) Se $A$ e $B$ são números ímpares e $C = 1$, então $A, \ B$ e $C$ satisfazem a equação.
   

Assinale a alternativa correta.