PUC-SP 2018 - Questões

Uma pessoa coloca, em seu celular, uma senha de 4 dígitos, todos diferentes de zero, de modo que o primeiro e o quarto dígitos sejam iguais, e o segundo dígito seja o dobro do terceiro. Sabendo que o segundo e o terceiro dígitos são sempre diferentes do primeiro, então o número de possibilidades que essa pessoa tem de montar essa senha é

Considere o retângulo $ABCD$, com $AB=a$ e o triângulo $EFG$, com $EG+ \dfrac{a}{2}, FC= \dfrac{a}{6}, FG=2 \sqrt{17}$ e $DG= \dfrac{a}{3}$ conforme mostra a figura.

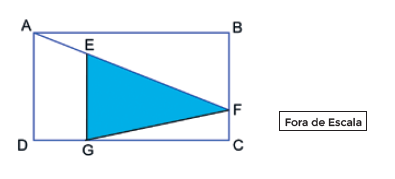
Sabendo que os pontos $A,E,F$ estão alinhados e que os pontos $F$ e $G$ pertencem, respectivamente, aos lados $\overline{BC}$ e $\overline{CD}$, a área do triângulo $EFG$, em unidades de área, é

A altura de um cone reto mede o dobro do raio de sua base. Se a área lateral desse cone é $9 \sqrt{5}\pi\ \text{cm}^2$, o volume do cone é

As coordenadas do vértice $(V)$ da parábola descrita pela função $f(x)=x^2-4x+3$ também pertencem à reta $r$, que é perpendicular à reta $s$, conforme mostra a figura.

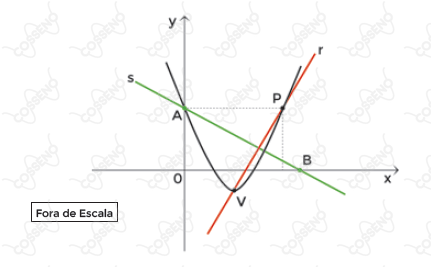
Sabendo que o ponto $A$ pertence à intersecção da reta $s$ com o eixo das ordenadas, então, a soma das coordenadas do ponto $B$, que pertence à intersecção da reta $s$ com o eixo das abscissas, é

As raízes da equação polinomial $x^3-x=0$ também são raízes do polinômio $p(x)=x^4-2x^3-x^2+kx$. O resto da divisão de $p(x)$ por $(x+2)$ é