PUC-SP 2012 Matemática - Questões

Felício e Jandira pretendem viajar e foram a uma casa de câmbio, onde receberam as seguintes informações: com os $3 060$ reais de que dispunha, Felício poderia comprar $1 500$ dólares e, com os $3 250$ reais de Jandira, seria possível comprar $1 250$ euros.

Com base nessas informações, é correto afirmar que, nesse dia, a cotação do euro em relação ao dólar era de

Certo dia, Adilson, Bento e Celso, funcionários de uma mesma empresa, receberam um lote de documentos para arquivar e dividiram o total de documentos entre eles, na razão inversa de suas respectivas idades: $24$, $30$ e $36$ anos. Se, ao completarem tal tarefa, foi observado que a soma dos documentos arquivados por Adilson e Celso excedia a quantidade arquivada por Bento em $26$ unidades, então o total de documentos do lote era um número

O fio de um rolo de arame tem $X$ metros de comprimento. Sabe-se que, usando todo o fio desse rolo, pode-se construir uma sucessão de $21$ circunferências tais que, a partir da segunda, a medida do raio de cada uma tem $2,5$ cm a mais do que a medida do raio da circunferência anterior. Se a área da região limitada pela terceira circunferência da sucessão é igual a $192 \ cm^2$, então, considerando a aproximação $\pi = 3$, é correto afirmar que

Suponha que no plano cartesiano mostrado na figura abaixo, em que a unidade de medida nos eixos coordenados é quilômetro, as retas $r$ e $s$ representam os trajetos percorridos por dois navios, $N_1$ e $N_2$, antes de ambos atracarem em uma ilha, localizada no ponto $I$.

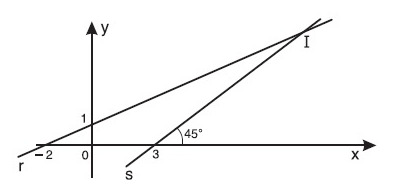
Considerando que, no momentos em que $N_1$ e $N_2$ se encontravam atracados em $I$, um terceiro navio, $N_3$, foi localizado no ponto de coordenadas $(26 ; 29)$, a quantos quilômetros $N_3$ distava de $I$?

Sabe-se que, em certo posto de combustível, as bombas de gasolina despejam o líquido à vazão constante de $3$ litros por minuto.

Certo dia, Lia parou nesse posto para abastecer seu carro quando ainda havia $10$ litros de gasolina no tanque e foram gastos $5$ minutos para colocar em seu interior mais alguns litros da gasolina, após o que ela seguiu sua viagem. Imediatamente após ter saído do posto, sabe-se que o carro de Lia:

• rodou ininterruptamente por $95$ minutos, quando, então, esgotou-se toda a gasolina do tanque e ele teve que parar;

• ao longo desses $95$ minutos, o volume de combustível no tanque, em litros, pode ser descrito como uma função do tempo t, em minutos, cujo gráfico é parte do ramo de uma parábola cujo vértice é o ponto $(100; 0).$

Considerando o intervalo $0 \leq t \leq 100$, em que $t = 0$ é o instante em que Lia parou no posto para colocar gasolina, então, se $V(t)$ é o volume de gasolina no tanque, em função do tempo $t$, em minutos, a expressão de $V(t)$, em litros, é