PUC-RJ 2017 - Questões

Temos uma urna com 100 bolas numeradas de 1 a 100.

1. a) Escolhendo duas bolas distintas simultaneamente, qual a probabilidade de que a soma seja 3?
   

2. b) Escolhendo duas bolas distintas simultaneamente, qual a probabilidade de que a soma seja menor ou igual a 7?
   

3. c) Escolhendo duas bolas distintas simultaneamente, qual a probabilidade de que o produto seja um número par?
   

Sejam $g_0$, $g_1:\mathbb{R}\to \mathbb{R}$ as seguintes funções:

$$g_{0} \left(x\right)=\dfrac{\left|x+2\right|-\left|x-2\right|}{2}$$ $g_{1} \left(x\right)=\dfrac{g_{0} \left(4x+6\right)+g_{0} \left(4x-6\right)}{2}$ w

1. a) Faça o esboço do gráfico de $g_0$.
   

2. b) Faça o esboço do gráfico de $g_1$
   

3. c) Resolva a inequação $g_{1} \left(x\right)\le \dfrac{x}{2}$.
   

Considere a parábola de equação $y=x^2-x+1$

1. a) Encontre os pontos de interseção da parábola com a reta de equação $y=x+1$.
   

2. b) Encontre $b$ para o qual a parábola intercepta a reta de equação $y=x+b$ em um único ponto.
   

3. c) Encontre as retas que passam pelo ponto $\left(1,\ 0\right)$ e que interceptam a parábola em um único ponto.
   

Uma lente convergente está representada esquematicamente na Figura. O objeto está localizado em $S_1=\frac{2}{3}\ {f}$, onde $f$ é a distância focal.

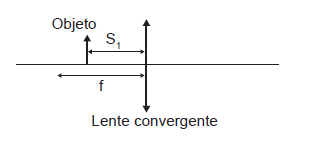
A distância da imagem à lente e o fator de ampliação são dados, respectivamente, por:

Um carro viaja a $100\ \text{km/h}$ por $15$ minutos e, então, baixa sua velocidade a $60\ \text{km/h}$, percorrendo $75\ \text{km}$ nesta velocidade.

Qual é a velocidade média do carro para o trajeto total, em $km/h$?