MACK 2018 Física - Questões

Olimpíadas de Inverno de Pyeongchang

No mês de fevereiro do vigente ano, do dia $7$ ao dia $25$, na cidade de Pyeongchang na Coreia do Sul, o mundo acompanhou a disputa de $2.952$ atletas, disputando $102$ provas de $15$ disciplinas esportivas na $23ª$ edição dos Jogos Olímpicos de Inverno. Praticamente todas as provas ocorreram sob temperaturas negativas, dentre elas, a belíssima patinação artística no gelo, que envolve um par de atletas. A foto acima mostra o italiano Ondrej Hotarek que, em meio à coreografia da prova, crava a ponta de um de seus patins em um ponto e gira a colega Valentina Marchei, cuja ponta de um dos patins desenha no gelo uma circunferência de raio $2,0$ metros. Supondo-se que a velocidade angular de Valentina seja constante e valha $6,2$ rad/s e considerando-se $\pi \cong 3,1$ , pode-se afirmar corretamente que o módulo da velocidade vetorial média da ponta dos patins de Valentina, ao percorrer de um ponto a outro diametralmente oposto da circunferência, vale, em $\text{m/s}$,

$c_{água}=1,0\ \text{cal/g}\ ^\circ\ C\ \text{(calor específico sensível da água)}$ $P_{água}=1,0\ \text{g/cm}^3\ \text{(massa específica da água)}$
$1,0\ \text{cal}=4,0\ \text{J}$

Para a prática de esportes olímpicos, é adequada a piscina olímpica. As dimensões dela, segundo Federação Internacional de Natação, devem ser de $50\ \text{m}$ para o comprimento; $25\ \text{m}$, para a largura, e $2,0\ \text{m}$, para a profundidade. A temperatura média ideal da água deve ser igual a $25\ ^\circ\ \text{C}$.

A quantidade de energia necessária, em joules, a ser fornecida para deixar a água da piscina na temperatura ideal – sendo essa a única troca de energia a se considerar –, observando que inicialmente a água, que preenche todo o volume da piscina, estava a $20\ ^\circ\ \text{C}$, é igual a

Com o intuito de facilitar seu trabalho, um operário construiu um artifício com cordas e polias fixas ideais e ainda uma barra homogênea de comprimento $L = 20\ \text{m}$, articulada no ponto $A$. A massa da barra vale $M_B = 60\ \text{kg}$ e o peso do bloco levantado tem módulo $Q = 500\ \text{N}$.

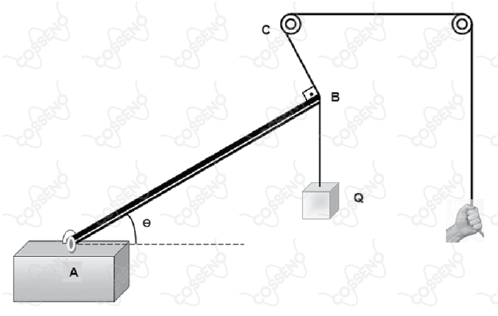
Considerando-se que o sistema está em equilíbrio no instante em que é retratado, que o módulo da aceleração gravitacional local seja $\text{g}\ = 10\, \text{m/s}^2$, que o trecho $BC$ da corda esteja perpendicular à barra e que o valor do ângulo é $\theta = 53\, ^\circ$, afirma-se corretamente que o módulo da reação horizontal da força na barra no ponto $A$ vale, em $N$ (newton),

$\begin{cases} \hspace{2pt}\mathrm{sen}\ 53 ^\circ = 0,80\\ \\ \cos\ 53 ^\circ =0,60 \end{cases}$

No dia vinte e três de janeiro de $2018$, a cidade de São Paulo ganhou a sua $72ª$ estação de metrô, a estação Higienópolis-Mackenzie que faz parte da Linha $4$ – Amarela. A estação é totalmente acessível aos usuários com deficiência e mobilidade reduzida. Os pavimentos contam com cinco elevadores que fazem a interligação da rua com o mezanino e com as plataformas, além de $26$ escadas rolantes e $13$ fixas. Suponha-se que uma pessoa com massa $80\ \text{kg}$ rejeite os elevadores e as escadas rolantes e, disposta a emagrecer dissipando a sua energia, suba diariamente os $25$ metros de profundidade da estação.

Considerando-se a massa específica da água $1,0\ \text{g/cm}^3$, seu calor específico sensível $1,0\ \text{cal/g}\ ^\circ\ \text{C}$, a aceleração gravitacional $\text{g}\ = 10\ \text{m/s}^2$ e $1,0\ \text{cal}$ equivalente aproximada a $4,0$ joules, em cinco dias, a energia dissipada por essa pessoa aquece um litro de água de um intervalo de temperatura em $^\circ \text{C}$ igual a

Um feixe de luz apresenta um comprimento de onda igual a $400\ \text{nm}$ quando se propaga no vácuo. Ao incidir em um determinado meio $X$, sua velocidade passa a ser $40\%$ menor que a velocidade de propagação da luz no vácuo. O índice de refração desse meio $X$ e o comprimento de onda do feixe no meio $X$ são, respectivamente,

(Obs.: considere a velocidade da luz no vácuo igual a $3,0 \cdot 10^8\ \text{m/s}$)