MACK 2011 Matemática - Questões

No intervalo $\left[0;\pi \right]$, seja $k$ o número de valores reais de $x$ tais que $\hspace{2pt}\mathrm{sen}^{2}\ x=\left|\cos\ x\right|$. Dessa forma,

Seja $t$ a reta bissetriz dos ângulos agudos formados pelas retas $\left(r\right) \, \sqrt{3}\cdot x+y-5=0$ e $\left(s\right) \, \sqrt{3}\cdot x-y-2=0$. Considere um ponto $B\in t$, cuja a distância à reta $s$ seja $3$. Dessa forma, a distância da intersecção das retas $r$ e $s$ à projeção de $B$ sobre $r$ é

Os valores de $k$, para que o sistema abaixo não tenha solução real, são os $2$ primeiros termos de uma progressão aritmética $(PA)$ de termos crescentes.

$$\left\{\begin{array}{l} {x-y+z=2} \\ \\{3x+ky+z=1} \\ \\{-x+y+kz=3} \end{array}\right.$$

Então, nessa $PA$, o logaritmo na base $\sqrt{3}$ do quadragésimo terceiro termo é

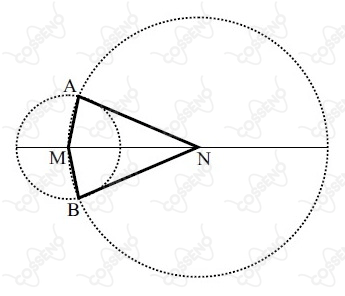
Na figura, os raios das circunferências de centros $M$ e $N$ são, respectivamente, $2r$ e $5r$. Se a área do quadrilátero $AMBN$ é $16\sqrt{6}$ , o valor de $r$ é

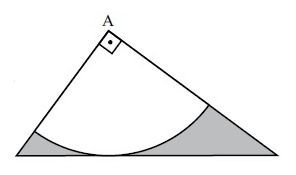
Na figura, os catetos do triângulo medem $3\ e\ 4$ e o arco de circunferência tem centro $A$. Dentre as alternativas, fazendo $\pi =3$, o valor mais próximo da área assinalada é: