ITA 2010 Física - Questões
Abrir Opções Avançadas
Pela teoria Newtoniana da gravitação, o potencial gravitacional devido ao Sol, assumindo simetria esférica, é dado por $-V=GM/r$, em que $r$ é a distância média do corpo ao centro do Sol. Segundo a teoria da relatividade de Einstein, essa equação de Newton deve ser corrigida para $-V=GM/r + A/r^2$, em que $A$ depende somente de $G$, de $M$ e da velocidade da luz, $c$. Com base na análise dimensional e considerando $k$ uma constante adimensional, assinale a opção que apresenta a expressão da constante $A$, seguida da ordem de grandeza da razão entre o termo de correção, $A/r^2$, obtido por Einstein, e o termo $GM/r$ da equação de Newton, na posição da Terra, sabendo a priori que $k=1$.
Considere a Terra como uma esfera homogênea de raio $R$ que gira com velocidade angular uniforme $\omega$ em torno do seu próprio eixo Norte-Sul. Na hipótese de ausência de rotação da Terra, sabe-se que a aceleração da gravidade seria dada por $g=GM/R^2$. Como $\omega \ne 0$, um corpo em repouso na superfície da Terra na realidade fica sujeito forçosamente a um peso aparente, que pode ser medido, por exemplo, por um dinamômetro, cuja direção pode não passar pelo centro do planeta. Então, o peso aparente de um corpo de massa $m$ em repouso na superfície da Terra a uma latitude $\lambda$ é dado por

Considere um segmento de reta que liga o centro de qualquer planeta do sistema solar ao centro do Sol. De acordo com a 2ª Lei de Kepler, tal segmento percorre areas iguais em tempos iguais. Considere, então, que em dado instante deixasse de existir o efeito da gravitação entre o Sol e o planeta.
Assinale a alternativa correta.
A temperatura para a qual a velocidade associada a energia cinética média de uma molécula de nitrogênio, $\ce{N2}$, é igual à velocidade de escape desta molécula da superfície da Terra é de, aproximadamente,
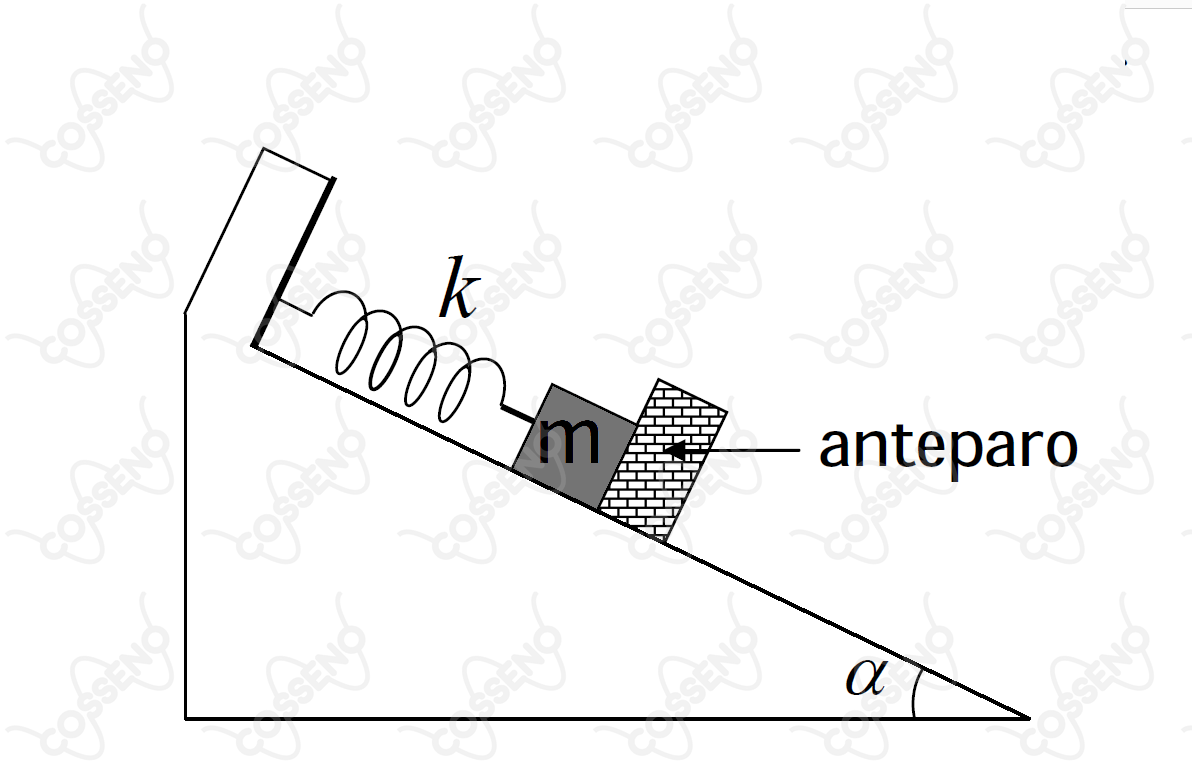
No plano inclinado, o corpo de massa $m$ é preso a uma mola de constante elástica $k$, sendo barrado a frente por um anteparo. Com a mola no seu comprimento natural, o anteparo, de alguma forma, inicia seu movimento de descida com uma aceleração constante $a$. Durante parte dessa descida, o anteparo mantém contato com o corpo, dele se separando somente após um certo tempo. Desconsiderando quaisquer atritos, podemos afirmar que a variação máxima do comprimento da mola é dada por
Carregando...