ITA 2005 Física - Questões

Filtro de Questões

Abrir Opções Avançadas

Filtrar por resolução:

01 ITA 2005 - Física

Quando camadas adjacentes de um fluido viscoso deslizam regularmente umas sobre as outras, o escoamento resultante e dito laminar. Sob certas condições, o aumento da velocidade provoca o regime de escoamento turbulento, que é caracterizado pelos movimentos irregulares (aleatórios) das partículas do fluido. Observa-se, experimentalmente, que o regime de escoamento (laminar ou turbulento) depende de um parâmetro adimensional (Número de Reynolds) dado por $R = \rho^{\alpha}v^{\beta}d^{\gamma}\eta^{\tau}$, em que $\rho$ é a densidade do fluido, $v$, sua velocidade, $\eta$, seu coeciente de viscosidade, e $d$, uma distância característica associada à geometria do meio que circunda o fluido. Por outro lado, num outro tipo de experimento, sabe-se que uma esfera, de diâmetro $D$, que se movimenta num meio fluido, sofre a ação de uma força de arrasto viscoso dada por $F = 3\ \pi\ D\ \eta\ v$.

Assim sendo, com relação aos respectivos valores de $\alpha,\ \beta,\ \gamma$ e $\tau$ uma das soluções é:

$\alpha = 1,\ \ \ \ \ \beta = 1,\ \ \ \ \ \gamma = 1,\ \ \ \ \ \tau = -1$.

$\alpha = 1,\ \ \ \ \ \beta = -1,\ \ \ \ \ \gamma = 1,\ \ \ \ \ \tau = 1$.

$\alpha = 1,\ \ \ \ \ \beta = 1,\ \ \ \ \ \gamma = 1,\ \ \ \ \ \tau = 1$.

$\alpha = -1,\ \ \ \ \ \beta = 1,\ \ \ \ \ \gamma = 1,\ \ \ \ \ \tau = 1$.

$\alpha = 1,\ \ \ \ \ \beta = 1,\ \ \ \ \ \gamma = 0,\ \ \ \ \ \tau = 1$.

02 ITA 2005 - Física

Um projetil de densidade $\rho _p$ é lançado com um ângulo $\alpha$ em relação à horizontal no interior de um recipiente vazio. A seguir, o recipiente é preenchido com um superfluido de densidade $\rho _s$, e o mesmo projetil é novamente lançado dentro dele, só que sob um ângulo $\beta$ em relação à horizontal. Observa-se, então, que, para uma velocidade inicial $\vec{v}$ do projetil, de mesmo módulo que a do experimento anterior, não se altera a distância alcançada pelo projétil (veja figura).

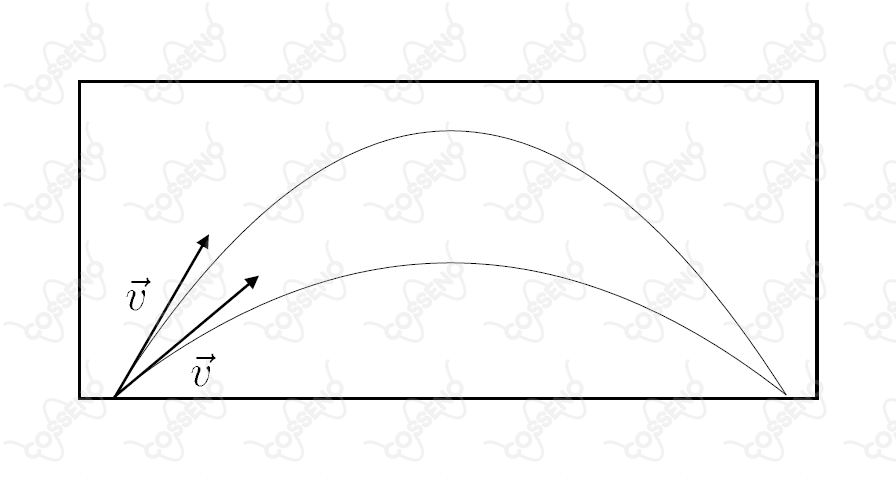
Sabendo que são nulas as forças de atrito num superfluido, podemos então afirmar, com relação ao ângulo de lançamento do projétil, que

$\cos\beta = (1 - \rho _s / \rho _p)\cos\alpha$

$\sin2\beta = (1 - \rho _s / \rho _p)\sin 2\alpha$

$\sin2\beta = (1 + \rho _s / \rho _p)\sin 2\alpha$

$\sin2\beta = \sin 2\alpha / (1 + \rho _s / \rho _p)$

$\cos2\beta = \cos \alpha / (1 + \rho _s / \rho _p)$

03 ITA 2005 - Física

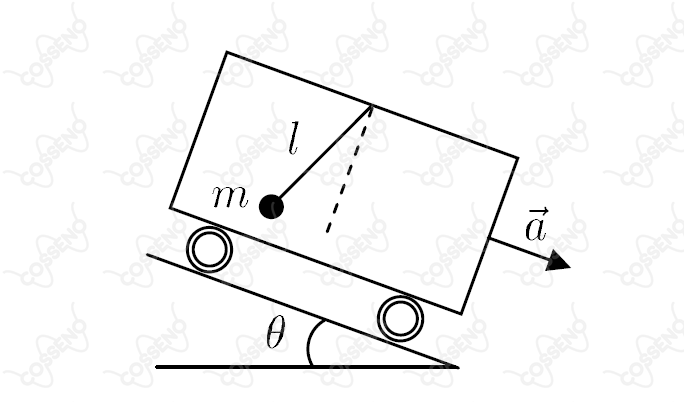
Considere uma rampa de ângulo $\theta$ com a horizontal sobre a qual desce um vagão, com aceleração $\vec{a}$, em cujo teto está dependurada uma mola de comprimento $l$, de massa desprezível e constante de mola $k$, tendo uma massa $m$ fixada na sua extremidade. Considerando que $l_0$ é o comprimento natural da mola e que o sistema está em repouso com relação ao vagão, pode-se dizer que a mola sofreu uma variação de comprimento $\Delta l = l - l_0$ dada por

$\Delta l = mg \sin\theta / k$

$\Delta l = mg \cos\theta / k$

$\Delta l = mg/k$

$\Delta l = m\sqrt{a^2 - 2ag\cos\theta + g^2} / k$

$\Delta l = m\sqrt{a^2 - 2ag\sin\theta + g^2} / k$

04 ITA 2005 - Física

Um objeto pontual de massa $m$ desliza com velocidade inicial $\vec{v}$, horizontal, do topo de uma esfera em repouso, de raio $R$. Ao escorregar pela superfície, o objeto sofre uma força de atrito de módulo constante dado por $f = 7mg/4\pi$. Para que o objeto se desprenda da superfície esférica após percorrer um arco de $60^{\circ}$ (veja figura), sua velocidade inicial deve ter o módulo de

05 ITA 2005 - Física

Um vagão-caçamba de massa $M$ se desprende da locomotiva e corre sobre trilhos horizontais com velocidade constante $v = 72{,}0 \text{ km/h}$ (portanto, sem resistência de qualquer espécie ao movimento). Em dado instante, a caçamba é preenchida com uma carga de grãos de massa igual a $4M$, despejada verticalmente a partir do repouso de uma altura de $6{,}00\ m$ (veja figura).

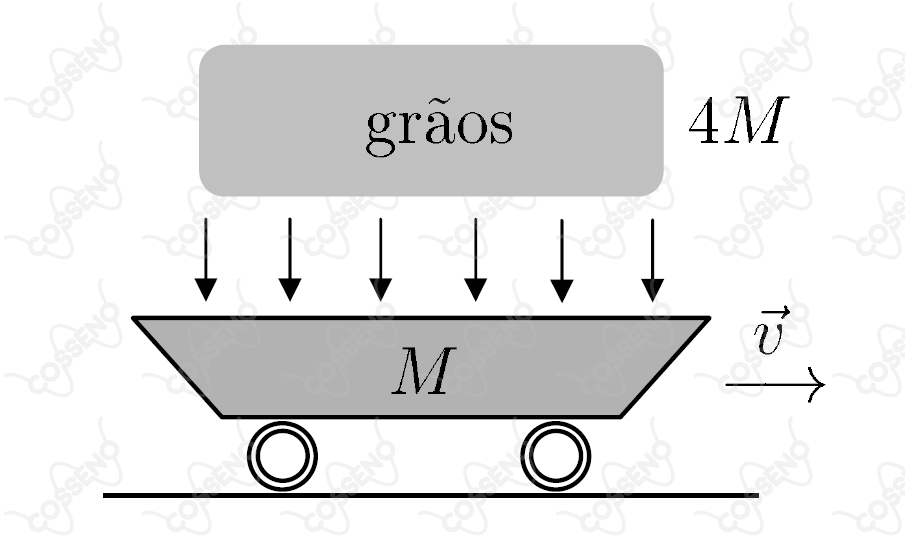
Supondo que toda a energia liberada no processo seja integralmente convertida em calor para o aquecimento exclusivo dos grãos, então, a quantidade de calor por unidade de massa recebido pelos grãos é

Carregando...