IME 2015 Física - Questões
Abrir Opções Avançadas
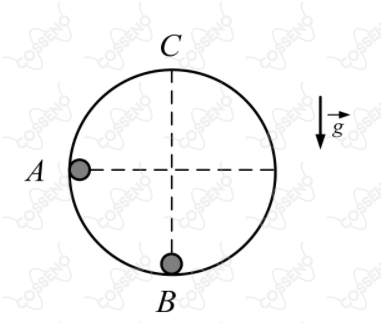
Um corpo puntiforme de massa $m_A$ parte de ponto $A$, percorrendo a rampa circular representada na figura acima, sem atrito, colide com outro corpo puntiforme de massa $m_B$, que se encontrava inicialmente em repouso no ponto $B$. Sabendo que este choque é perfeitamente inelástico e que o corpo resultante deste choque atinge o ponto $C$ , ponto mais alto da rampa, com a menor velocidade possível mantendo o contato com a rampa, a velocidade inicial do corpo no ponto $A$, em $m/s$, é
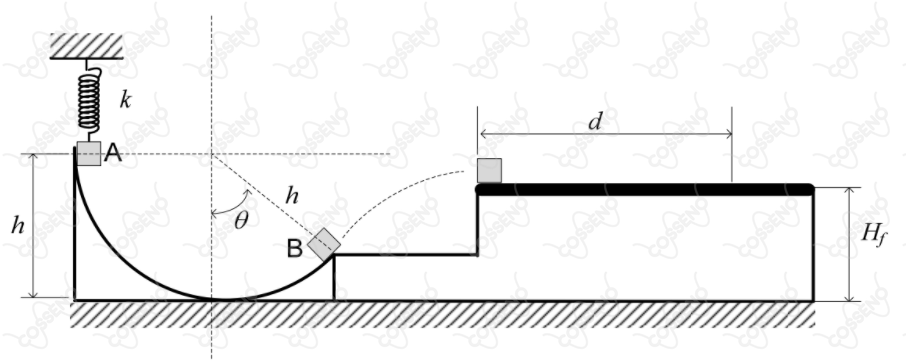
Uma mola comprimida por uma deformação $x$ está em contato com um corpo de massa $m$, que se encontra inicialmente em repouso no Ponto $A$ da rampa circular. O corpo é liberado e inicia um movimento sem atrito na rampa. Ao atingir o ponto $B$ sob um ângulo $\theta$ indicado na figura, o corpo abandona a superfície da rampa. No ponto mais alto da trajetória, entra em contato com uma superfície plana horizontal com coeficiente de atrito cinético $\mu$. Após deslocar-se por uma distância $d$ nesta superfície horizontal, o corpo atinge o repouso. Determine, em função dos parâmetros mencionados:
a) a altura final do corpo $H_f$ em relação ao solo;
b) a distância $d$ percorrida ao longo da superfície plana horizontal.
- aceleração da gravidade: $g$;
- constante elástica da mola: $k$;
- raio da rampa circular: $h$.
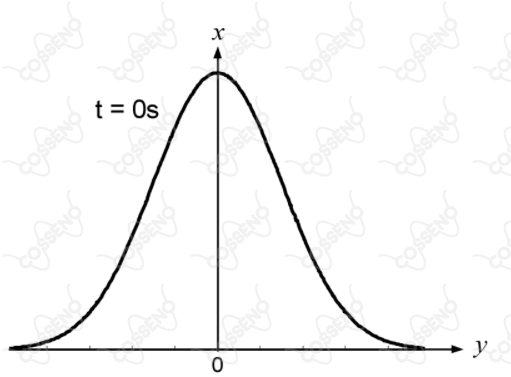
A figura acima mostra uma onda transversal na forma de um pulso ondulatório em uma corda esticada. A onda está se propagando no sentido positivo do eixo $x$ com velocidade igual a $0,5 \ m/s$. Se o deslocamento $y$, em metros, para uma coordenada $x$, em metros, no instante $t = 0$ é dado por $$ y(x) = \frac{1}{x^2+4}$$ o deslocamento $y$, em centímetros, para $x = 3$ metros e $t = 2$ segundos é
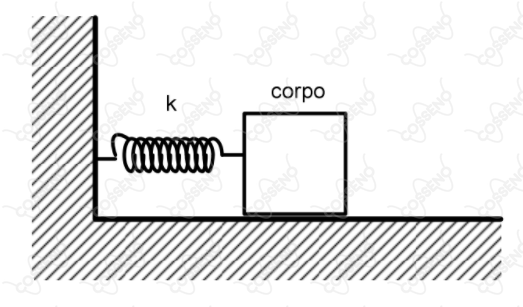
Um corpo com massa $m$, inicialmente em repouso sobre uma superfície horizontal e preso a uma mola de constante elástica $k$, representado na figura, recebe um impulso $I$, para a direita, dando início a um Movimento Harmônico Simples (MHS). Inicialmente não existe atrito entre o corpo e a superfície horizontal devido à presença de um lubrificante. Contudo, após $1000$ ciclos do MHS, o lubrificante perde eficiência e passa a existir atrito constante entre o corpo e a superfície horizontal. Diante do exposto, determine:
a) a máxima amplitude de oscilação;
b) o módulo da aceleração máxima;
c) a máxima energia potencial elástica;
d) a distância total percorrida pelo corpo até que este pare definitivamente.
- massa do corpo: $m = 2 \ kg$;
- impulso aplicado ao corpo: $I = 4 \ kg \cdot m/s$;
- constante elástica da mola: $k = 8 \ N/m$;
- coeficiente de atrito: $\mu = 0{,}1$;
- aceleração da gravidade: $g = 10 \ m/s^2$.
Observação:
- a massa da mola é desprezível em relação à massa do corpo.
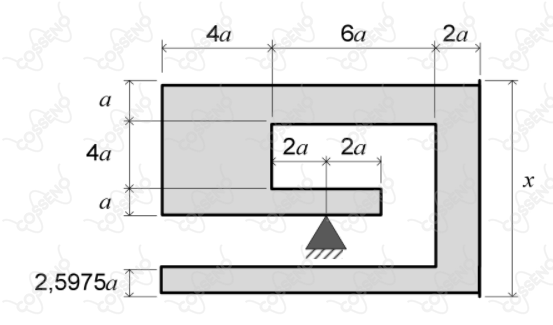
Uma chapa rígida e homogênea encontra-se em equilíbrio. Com base nas dimensões apresentadas na figura, o valor da razão $x/a$ é
Carregando...