IME 2009 Matemática - Questões
Abrir Opções Avançadas
Sejam dois conjuntos, $\text{X}$ e $\text{Y}$, e a operação $\Delta$, definida por$$\text{X}\Delta \text{Y} = \text{(X – Y)}\cup\text{(Y – X)}$$
Pode-se afirmar que
Sabe-se que:
$a = [a] + \{a\}{,} \ \forall a \in \mathbb{R}$, onde $[a]$ é a parte inteira de $a$
$\begin{cases} x + [ \ y \ ] +\{ \ z \ \} = 4{,}2 \\ y+ [ \ z \ ] + \{ \ x \ \} = 3{,}6 \ , \ com \ x{,} \ y \ e \ z \in \mathbb{R} \\ z + [ \ x \ ] + \{ \ y \ \} = 2 \end{cases}$
Determine o valor de $x - y + z$.
Seja $z=\rho\cdot e^{i\theta}$ um número complexo onde $\rho$ e $\theta$ são, respectivamente, o módulo e o argumento de $z$ e $i$ é a unidade imaginária. Sabe-se que $\rho = 2a\cos\theta$, onde $a$ é uma constante real positiva. A representação de $z$ no plano complexo é
I
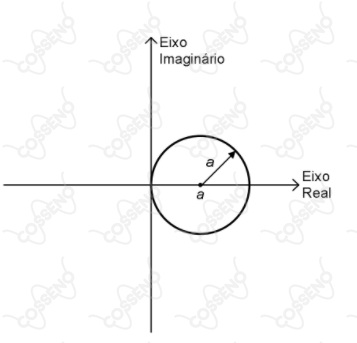
II

III
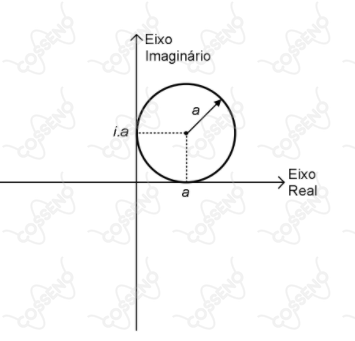
IV
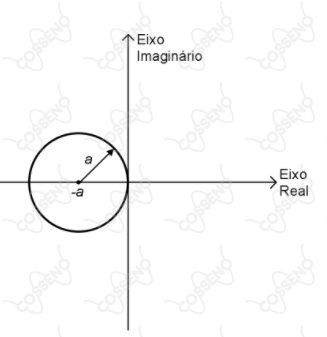
V
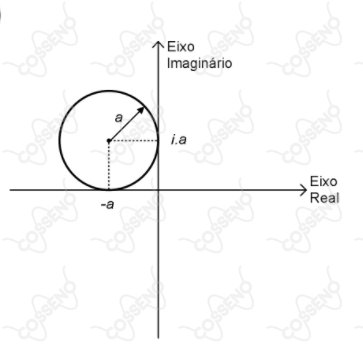
Um triângulo isósceles possui seus vértices da base sobre o eixo das abscissas e o terceiro vértice, $B$, sobre o eixo positivo das ordenadas. Sabe-se que a base mede $b$ e seu ângulo oposto o $B = 120^{\circ}$. Considere o lugar geométrico dos pontos cujo quadrado da distância à reta suporte da base do triângulo é igual ao produto das distâncias as outras duas retas que suportam os dois outros lados. Determine a(s) equação(ões) do lugar geométrico e identifique a(s) curva(s) descrita(s).
Seja $\text{A}$ uma matriz quadrada inversível de ordem $4$ tal que o resultado da soma $(\text{A}^4 + 3\text{A}^3)$ é uma matriz de elementos nulos. O valor do determinante de $\text{A}$ é
Carregando...