IME 2009 - Questões
Abrir Opções Avançadas
O par ordenado $(x,y)$, com $x$ e $y$ inteiros positivos, satisfaz a equação $5x^2+2y=11(xy-11)$. O valor de $x+y$ é
Seja $\text{A}$ uma matriz quadrada inversível de ordem $4$ tal que o resultado da soma $(\text{A}^4 + 3\text{A}^3)$ é uma matriz de elementos nulos. O valor do determinante de $\text{A}$ é
Sabe-se que $\displaystyle y=\frac{2+2^{\cos2x}}{2(1+4^{\sin^2x})}, \forall x\in \mathbb{R}$. Uma outra expressão para $y$ é
Os centros das faces de um tetraedro regular são os vértices de um tetraedro interno. Se a razão entre os volumes dos tetraedros interno e original vale $\frac{m}{n}$, onde $m$ e $n$ são inteiros positivos primos entre si, o valor de $m+n$ é
Seja $z=\rho\cdot e^{i\theta}$ um número complexo onde $\rho$ e $\theta$ são, respectivamente, o módulo e o argumento de $z$ e $i$ é a unidade imaginária. Sabe-se que $\rho = 2a\cos\theta$, onde $a$ é uma constante real positiva. A representação de $z$ no plano complexo é
I
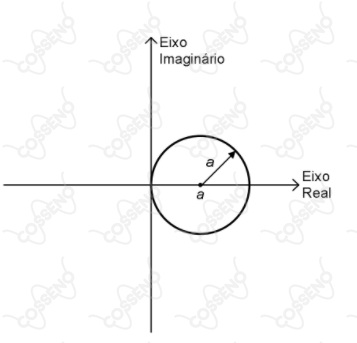
II

III
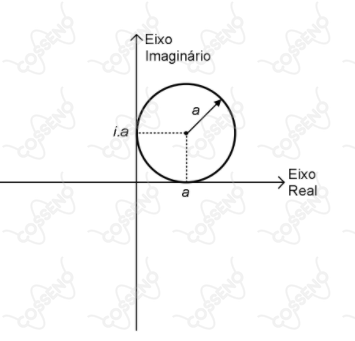
IV
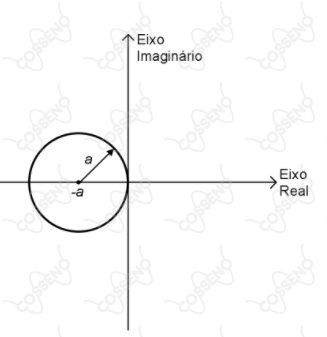
V
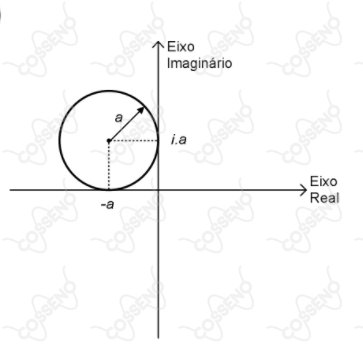
Carregando...