IME 2003 Matemática - Questões
Abrir Opções Avançadas
Seja $z$ um número complexo de módulo unitário que satisfaz a condição $z^{2n} \neq -1$, onde $n$ é um número inteiro positivo. Demonstre que $\frac{z^n}{1 + z^{2n}}$ é um número real.
Determine todos os valores reais de $x$ que satisfazem a equação:
$| \log{(12x^3 - 19x^2 + 8x)}| = \log{(12x^3 - 19x^2 + 8x)}$
onde $\log{(y)}$ e $|y|$ representam, respectivamente, o logaritmo na base $10$ e o módulo de $y$.
Dada numa circunferência de raio $R$, inscreve-se nela um quadrado. A seguir, inscreve-se uma circunferência neste quadrado. Este processo se repete indefinidamente para o interior da figura de maneira que cada quadrado estará sempre inscrito em uma circunferência e simultaneamente circunscrito por outra. Calcule, em função de $R$, a soma das áreas delimitadas pelos lados dos quadrados e pelas circunferências que os circunscrevem, conforme mostra a figura.

Resolva a equação $\tan{(\alpha)} + \tan{(2 \alpha)} = 2 \cdot \tan{(3 \alpha)}$, sabendo-se que $\alpha \in [0{,} \ {{\pi}/{2}})$.
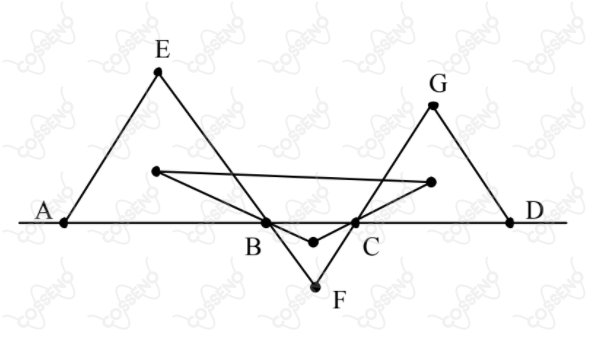
Sobre uma reta $r$ são marcados os pontos $A$, $B$, $C$ e $D$. São construídos os triângulos equiláteros $ABE$ $BCF$ e $CDG$, de forma que os pontos $E$ e $G$ se encontram do mesmo lado da reta $r$, enquanto que o ponto $F$ se encontra do lado oposto, conforme mostra a figura. Calcule a área do triângulo formado pelos baricentros de $ABE$, $BCF$ e $CDG$ em função dos comprimentos dos segmentos $AB$, $BC$ e $CD$.
Carregando...