IME 2000 Matemática - Questões
Abrir Opções Avançadas
Calcule o determinante:
$$D =\begin{bmatrix} 1&1&1&1&1&1&1 \\ 1&3&1&1&1&1&1 \\ 1&1&5&1&1&1&1 \\1&1&1&7&1&1&1 \\ 1&1&1&1&9&1&1 \\ 1&1&1&1&1&11&1\\ 1&1&1&1&1&1&13\end{bmatrix}$$
Considere $a$, $b$, e $c$ números reais tais que $a<b<c$. Prove que a equação abaixo possui exatamente duas raízes, $x_1$ e $x_2$, que satisfazem a condição: $a<x_1<b<x_2<c$. $$\frac{1}{x-a}+\frac{1}{x-b}+\frac{1}{x-c}=0$$
Represente graficamente a função: $$F(\theta)=\frac{1}{1+\sin^2 \theta}+\frac{1}{1+\cos^2 \theta}+\frac{1}{1+\sec^2 \theta}+\frac{1}{1+\csc^2 \theta}$$
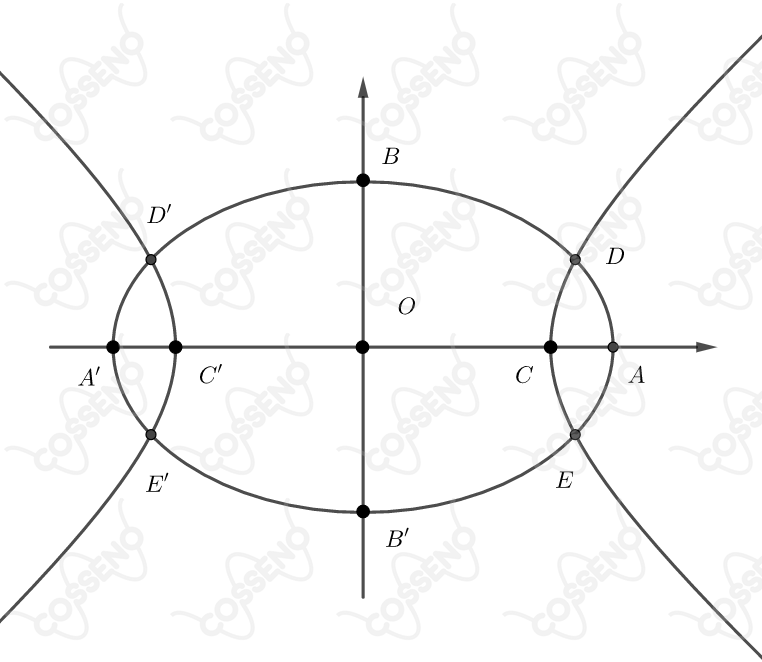
Calcule as coordenadas dos pontos de interseção da elipse com a hipérbole, representadas na figura abaixo, sabendo-se que:
os pontos $C$ e $C^\prime$ são os focos da elipse e os pontos $A$ e $A^\prime$ são os focos da hipérbole;
$BB^\prime$ é o eixo conjugado da hipérbole;
$OB = OB^\prime = 3 m$ e $OC = OC^\prime = 4 m$.
Determine o polinômio em $n$, com no máximo $4$ termos, que representa o somatório dos quadrados dos $n$ primeiros números naturais. $$\sum_{k=1}^{n}{k^2}$$
Carregando...