IME 1992 - Questões
Abrir Opções Avançadas
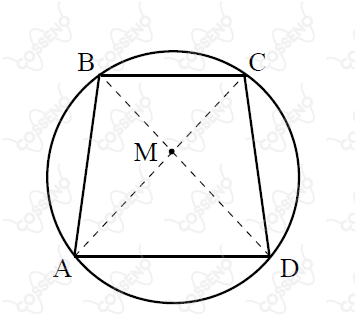
Dado o quadrilátero $ABCD$, inscrito num círculo de raio $r$, conforme a figura abaixo, prove que:$$\frac{AC}{BD} = \frac{AB\cdot AD + BC\cdot CD} {AB\cdot BC + CD\cdot AD}$$
Determine a equação da reta que passa por um dos vértices da curva definida por $4y^2 + 8y – x^2 = 4$, formando um ângulo de $45^\circ$ com o eixo horizontal.
A partir da função $R(t) = e^{-At} +\frac{A}{B - A}\left(e^{-At} - e^{-Bt} \right)$, onde $t$ é variável (tempo) e $A$ e $B$ são constantes reais, encontre a expressão de $R(t)$, para o caso em que $A$ tende a $B$ de modo que $R(t)$ seja uma função contínua.
Encontre todas as soluções de:$$ \sec x - 2 \cos x = 1 \ \ \text{ em $[0, 2\pi]$}$$
Calcule o valor do determinante abaixo:$$D_n =\begin{vmatrix}m+x& m& m& m& \cdots& m \\ m& m+x& m& m& \cdots & m \\ m& m& m+x& m& \cdots & m \\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\m& m& m&m& \cdots& m+x \end{vmatrix}$$
Carregando...